The time period of a bar pendulum when suspended at distance 30cm and 50cm from its centre of gravity comes out to be the same. If the mass of the body is 2kg. Find out its moment of inertia about an axis passing through first point.
_S01_024_Q01.png)
IA=MK2+M12 but l1=50cm & K2l1=30cm⇒K2=30×50cm2
IA=2×(30×50×10−4)+2×(50×10−2)2=0.3+0.5=0.5=0.8kg−m2
Question based on calculation of time period by energy method.
_S01_024_S01.png)
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise-01117videos
SIMPLE HARMONIC MOTION
- BOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise-0219videos
SIMPLE HARMONIC MOTION
- BOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)25videos
RACE
- BOOK - ALLENCHAPTER - TEST PAPEREXERCISE - PHYSICS4videos
TEST PAPER
Similar Questions
A solid cylinder of uniform density of radius 2 cm has mass of 50 g. If its length is 12 cm, calculate its moment of inertia about an axis passing through its centre and perpendicular to its length.
View SolutionTwo masses m1andm2 are placed at a distance r from each other. Find out the moment of inertia of system about an axis passing through their centre of mass.
View Solution
Knowledge Check
- Question 1 - Select One
A cylinder of 500 g and radius 10 cm has moment of inertia about an axis passing through its centre and parallel to its length is
A2.5×10−3kgm2B2×10−3kgm2C5×10−3kgm2D3.5×10−3kgm2 - Question 2 - Select One
The mass of a body cannot be considered to be concentrated at the centre of mass of the body for the purpose of computing its moment of inertia.
For then the moment of inertia of every body about an axis passing through its centre of mass would be zero.AStatement-1 is True, Statement-2 is Ture , Statement -2 is a correct explanation for statement -1.BStatement-1 is True, Statement-2 is True , Statement-2 is NOT a correct explanation fro Statement -1.CStatement-1 is True, Statement-2 is False.DStatement-1 is False, Statement-2 is True. - Question 3 - Select One
A solid cylinder has diameter D and length L. Find its moment of inertia about an axis perpendicular to its length and passing through the centre of gravity.
AM[D24+L212]BM[D216+L2!2]CM[D28+L212]DM[D24+L26]
A body of mass 200g oscillates about a horizontal axis at a distance of 20cm from its centre of gravity . If the length of the equivalent simple pendulum is 35cm, find its moment of inertia about the point of suspension.
View SolutionA square of a side a is cut from a square of side 2a as shown in the figure. Mass of this square with a hole is M. Then its moment of inertia about an axis passing through its centre of mass and perpendicular to its plane will be
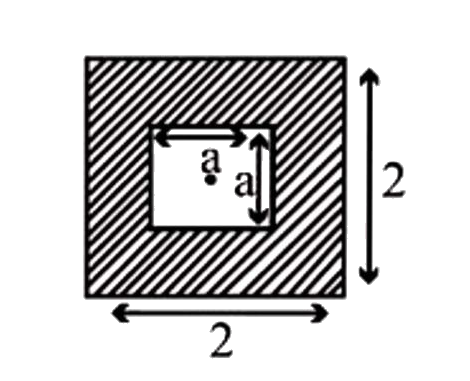 View Solution
View SolutionA body of mass 0.2 kg oscillates about a horizental axis at a distance 20 cm from its centre ofr gravity. Ifd the length of the equivalent simple pendulem be 0.35 m, find the moment of inertia about the axis of suspension.
View SolutionCalculate the moment of inertia of a ring of mass 2 kg and radius 50 cm about an axis passing through its centre and perpendicular to its plane
View SolutionCalculate the moment of inertia of a ring of mass 2kg and radius 2cm about an axis passing through its centre and perpendicular to its surface.
View Solution

