A 100g block is connected to a horizontal massless spring of force constant 25.6N/m. The block is free to oscillate on a horizontal fricationless surface. The block is displced by 3cm from the equilibrium position, and at t=0, it si released from rest at x=0, The position-time graph of motion of the block is shown in figure.
_S01_052_Q01.png)
Let us now make a slight change to the initial conditions. At t=0, let the block be released from the same position with an initial velocity v1=64cm/s. Position of the block as a function of time can be expressed as
x=5sin16t
x=5sin(16t+37∘)
x=5sin(16t−37∘)
x=5cos(16t+37∘)
The correct Answer is:B
Let x=Asin(16t+ϕ)v=Aωcos(16t+ϕ) where ω2=Km=25.60.1=256⇒ω=16radsec
Att=0,3=Asinϕ & 64=Acosϕ⇒tanϕ=34⇒ϕ=37∘ Also A=5cm
Therefore equation of SHM x=5sin(16t+37∘)
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBook:ALLENChapter:SIMPLE HARMONIC MOTIONExercise:Exercise-01
Explore 117 Videos
- SIMPLE HARMONIC MOTIONBook:ALLENChapter:SIMPLE HARMONIC MOTIONExercise:Exercise-02
Explore 19 Videos
- RACEBook:ALLENChapter:RACEExercise:Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)
Explore 25 Videos
- TEST PAPERBook:ALLENChapter:TEST PAPERExercise:PHYSICS
Explore 4 Videos
Similar Questions
A block of mass m is connected to another .block of mass M by a massless spring of spring constant k. A constant force f starts action as shown in figure, then:

View SolutionA block of mass m is connected with two ideal pullies and a massless spring of spring constant K as shown in figure. The block is slightly displaced from its equilibrium position. If the time period of oscillation is μπ√mK. Then find the value of μ.
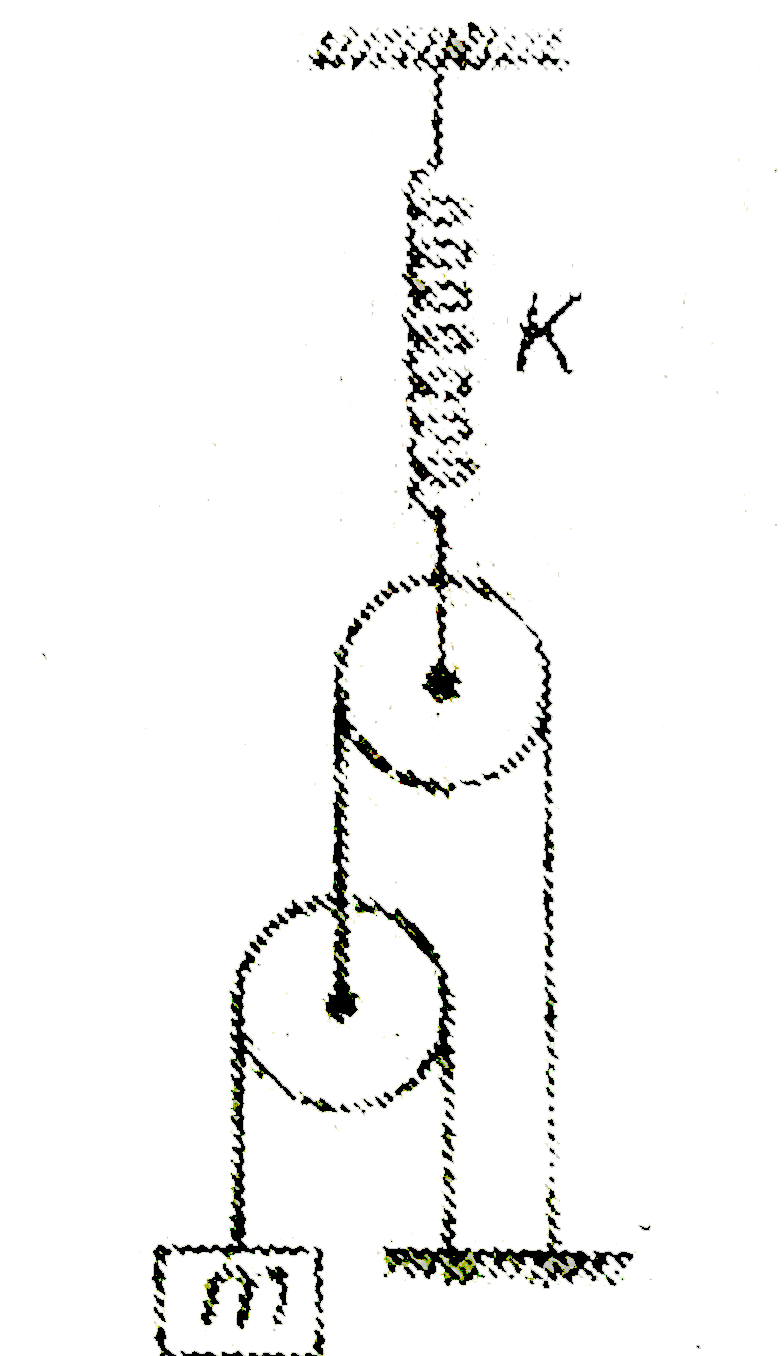
View Solution
Knowledge Check
A 100g block is connected to a horizontal massless spring of force constant 25.6N/m. The block is free to oscillate on a horizontal fricationless surface. The block is displced by 3cm from the equilibrium position, and at t=0, it si released from rest at x=0, The position-time graph of motion of the block is shown in figure.
_S01_050_Q01.png)
When the block is at position A on the graph, itsAposition and velocity both are negativeBposition and velocity both are positive.Cposition is negative and velocity is positive.Dposition is positive and velocity is negative.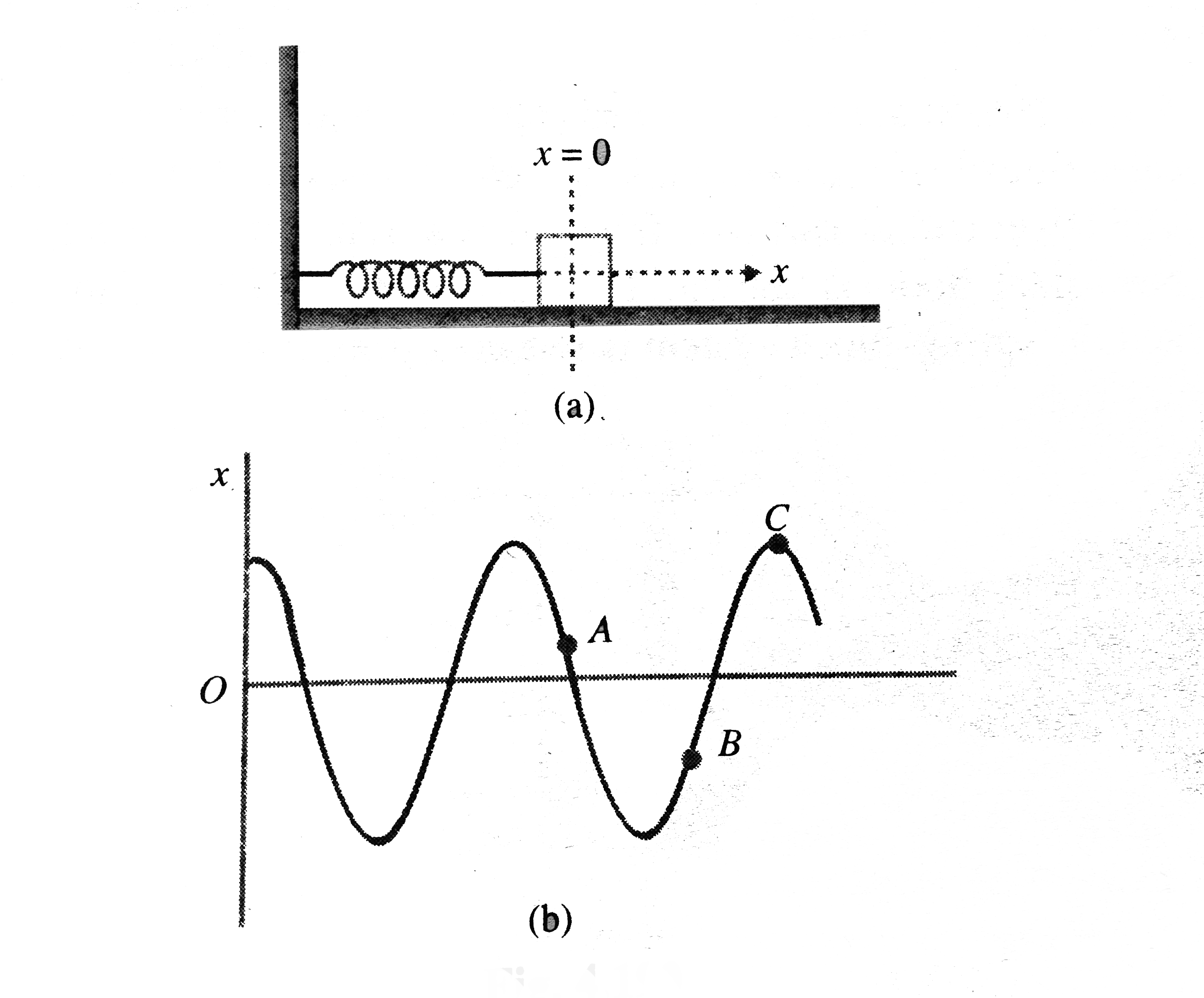
A 100 g block is connected to a horizontal massless spring of force constant 25.6Nm As shown in Fig. the block is free to oscillate on a horizontal frictionless surface. The block is displaced 3 cm from the equilibrium position and , at t=0, it is released from rest at x=0 It executes simple harmonic motion with the postive x−direction∈decated∈Fig.Thepositiontime(x-t) graph of motion of the block is as shown in Fig.
Q. When the block is at position A on the graph, itsAposition and velocity both are negativeBposition is positive and velocity is negativeCposition is negative and velocity is positiveDposition and velocity both the positive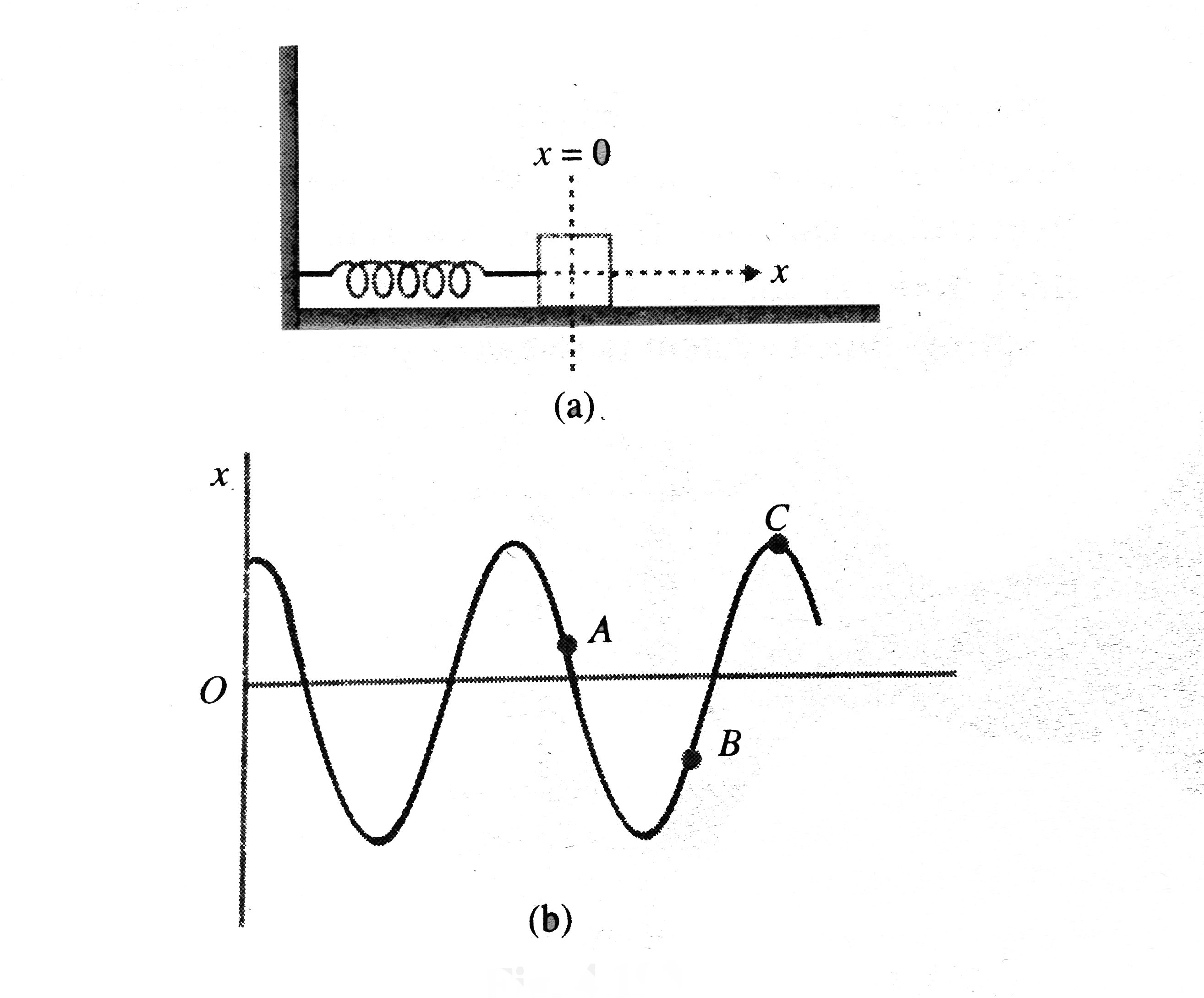
A 100 g block is connected to a horizontal massless spring of force constant 25.6Nm As shown in Fig. the block is free to oscillate on a horizontal frictionless surface. The block is displaced 3 cm from the equilibrium position and , at t=0, it is released from rest at x=0 It executes simple harmonic motion with the postive x-direction indecated in Fig. The position time (x−t) graph of motion of the block is as shown in Fig.
Q. When the block is at position B on the graph its.Aposition and velocity both are positive.Bposition is positive and velocity is negativeCposition is negative and velocity is positiveDosition and velocity are negative.
Two blocks rest on a smooth horizontal surface. They are connected by a spring of force constant k. If the system is set into oscillation find its time period.

View SolutionA block whose mass m is 680g is fastened to a spring whose spring constant k is 65N/m. The block is pulled a distance x=11cm from its equilibrium position at x=0 on a frictionless surface and released from rest at t= 0.
What is the phase constant ϕ for the motion?
View Solution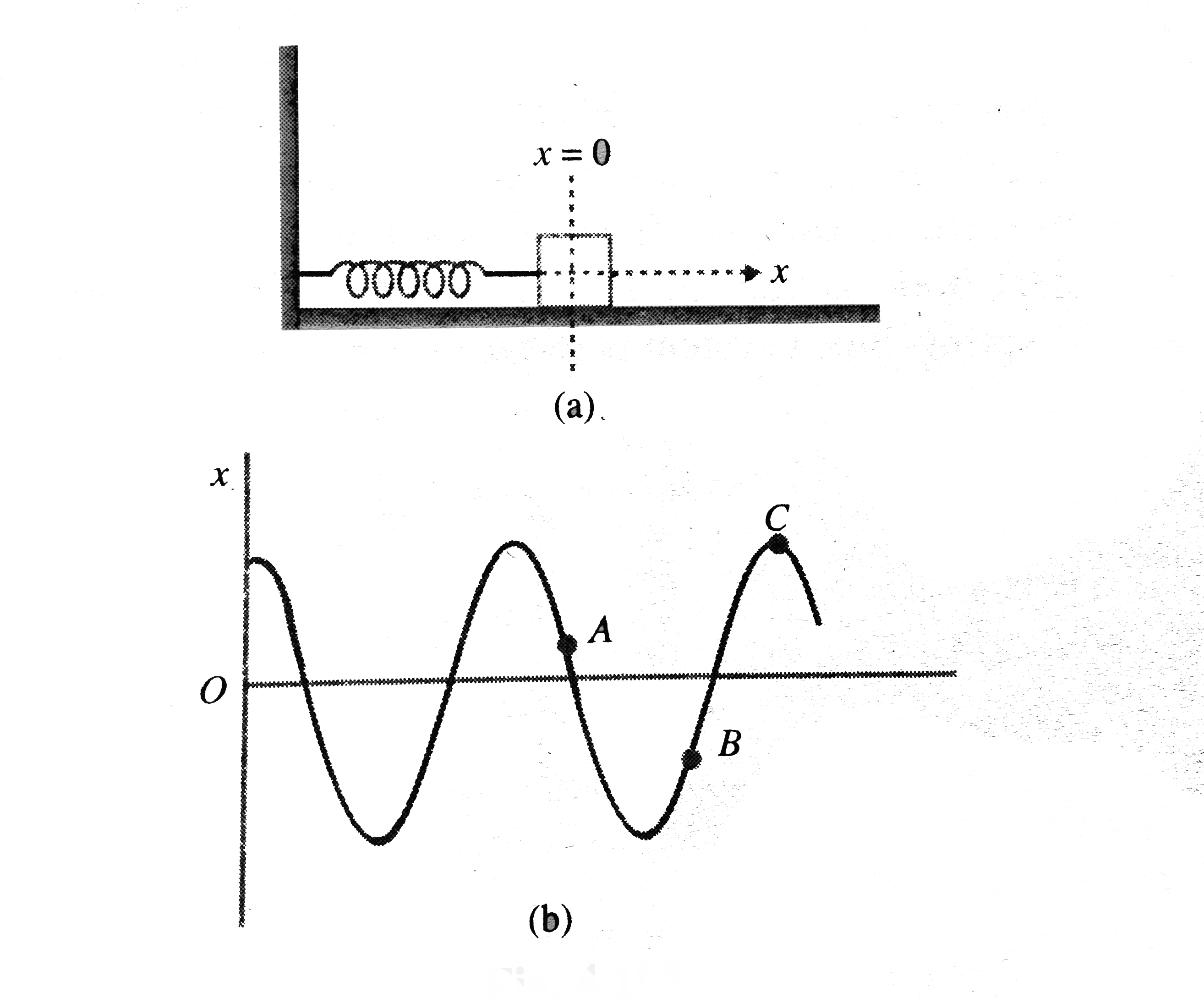
A 100 g block is connected to a horizontal massless spring of force constant 25.6Nm As shown in Fig. the block is free to oscillate on a horizontal frictionless surface. The block is displaced 3 cm from the equilibrium position and , at t=0, it is released from rest at x=0 It executes simple harmonic motion with the postive x-direction indecated in Fig. The position time (x−t) graph of motion of the block is as shown in Fig.
When the block is at position C on the graph, its
View Solution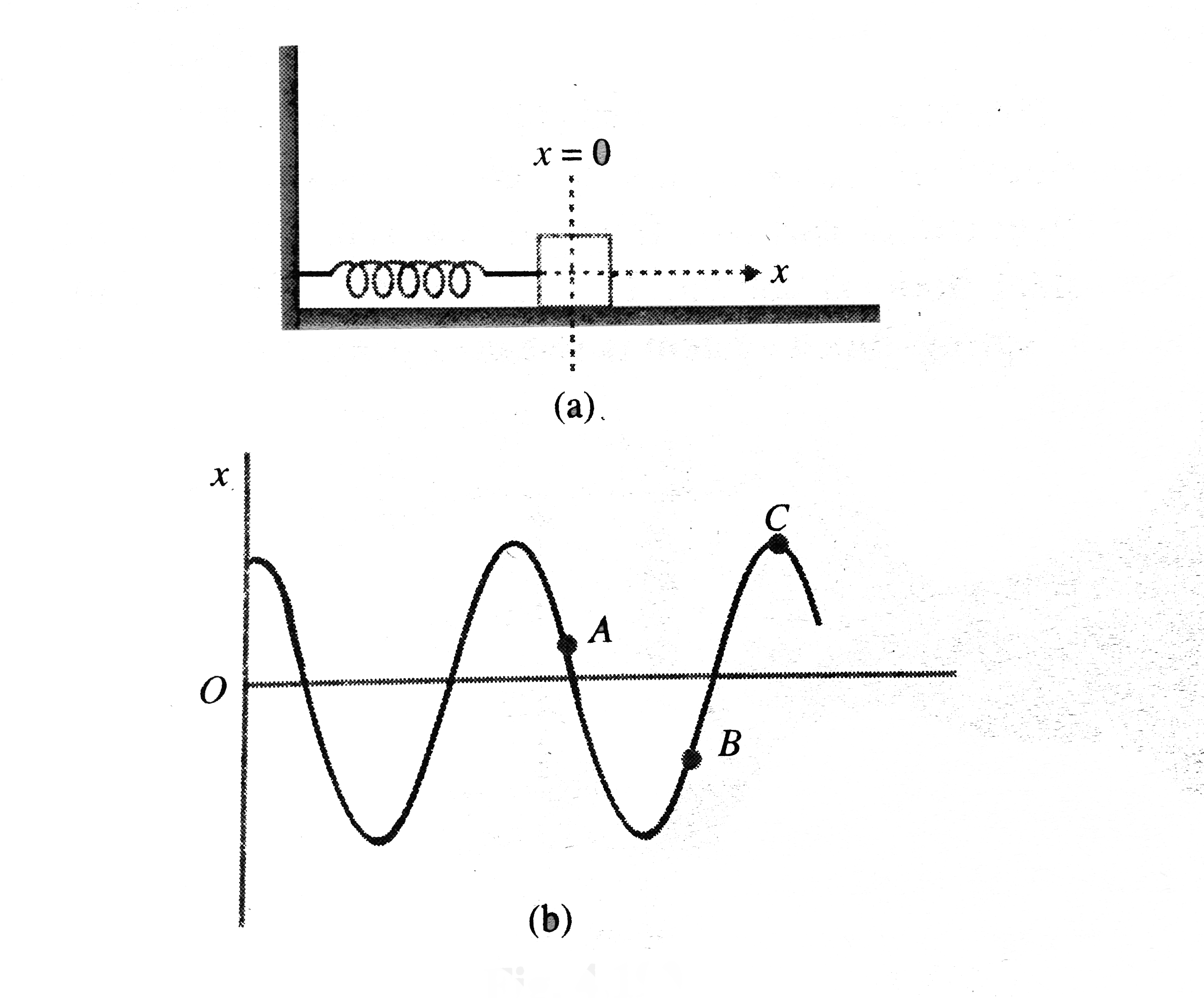
A 100 g block is connected to a horizontal massless spring of force constant 25.6Nm As shown in Fig. the block is free to oscillate on a horizontal frictionless surface. The block is displaced 3 cm from the equilibrium position and , at t=0, it is released from rest at x=0 It executes simple harmonic motion with the postive x-direction indecated in Fig. The position time (x−t) graph of motion of the block is as shown in Fig.
Position of the block as a function of time can now be expressed as
View Solution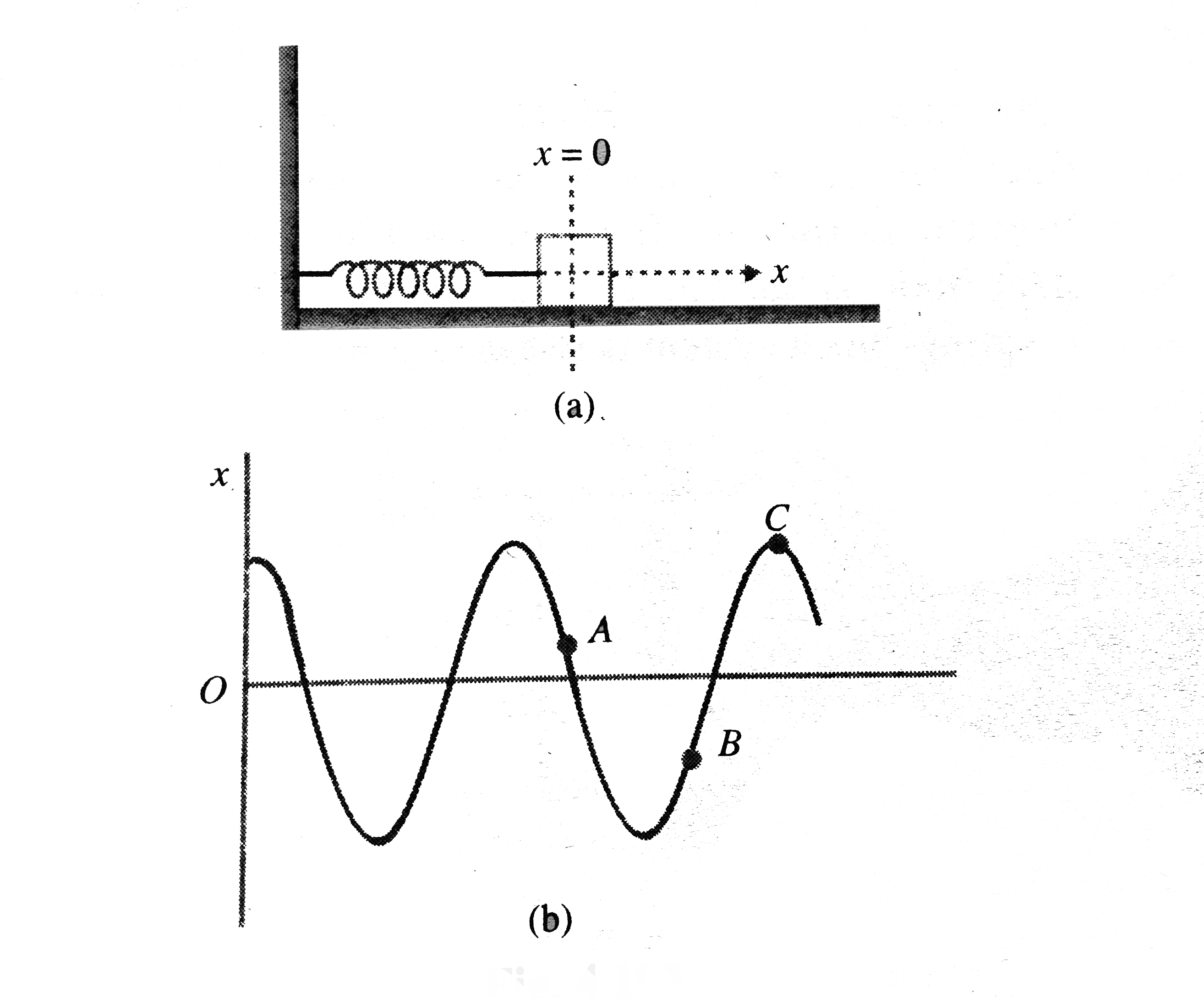
A 100 g block is connected to a horizontal massless spring of force constant 25.6Nm As shown in Fig. the block is free to oscillate on a horizontal frictionless surface. The block is displaced 3 cm from the equilibrium position and , at t=0, it is released from rest at x=0 It executes simple harmonic motion with the postive x-direction indecated in Fig. The position time (x−t) graph of motion of the block is as shown in Fig.
Velocity of the block as a function of time can be expressed as
View Solution