The mass (M) shown in the figure oscillates in simple harmonic motion with amplitude of the point (P) is.
(##JMA_CHMO_C10_010_Q01##).

A

$\frac{k_{1} A}{k_{2}}$

B

$\frac{k_{2} A}{k_{1}}$

C

$\frac{k_{1} A}{k_{1} + k_{2}}$

D

$\frac{k_{2} A}{k_{1} + k_{2}}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

In series force remain same, if extension in $k_{1}$ and $k_{2}$ are $x_{1}$ and $x_{2}$ respectively.
Then $k_{1} x_{1} = k_{2} x_{2} \Rightarrow x_{1} + x_{2} = A$
$\Rightarrow x_{1} + \frac{k_{1} x_{1}}{k_{2}} = A \Rightarrow x_{1} \frac{k_{1} + k_{2}}{k_{2}} = A$
$\Rightarrow x_{1} = \frac{k_{2} A}{(k_{1} + k_{2})}$
Amplitude of point P will be the max, ext. in $k_{1}$ .
So amplitude of point P is $\frac{k_{2} A}{k_{1} + k_{2}}$

|

Updated on:21/07/2023

Class 12 PHYSICS SIMPLE HARMONIC MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The mass M shown in figure ocillates in simple harmonic motion with amplitude A.
The amplitude of the point P is

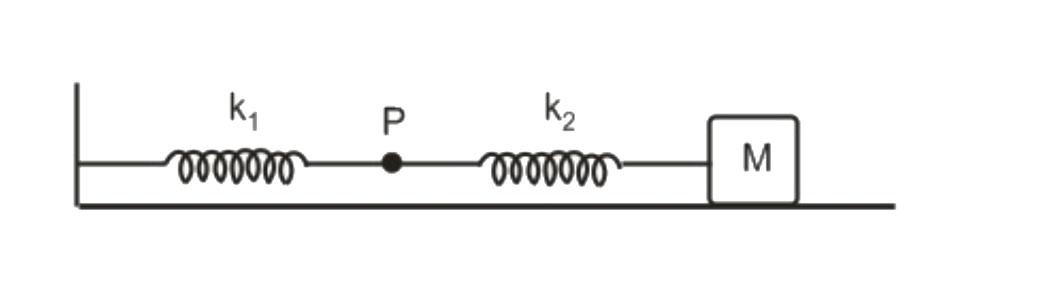A $\frac{k_{1} A}{k_{2}}$
B $\frac{k_{2} A}{k_{2} - k_{1}}$
C $\frac{k_{2} A}{k_{1} + k_{2}}$
D $\frac{k_{2} A}{k_{1}}$
Question 2 - Select One
The mass $M$ shown in the figure oscillates in simple harmnonic motion and amplitude $A$ . The amplitude of the point $P$ is

A $\frac{k_{1} A}{k_{2}}$
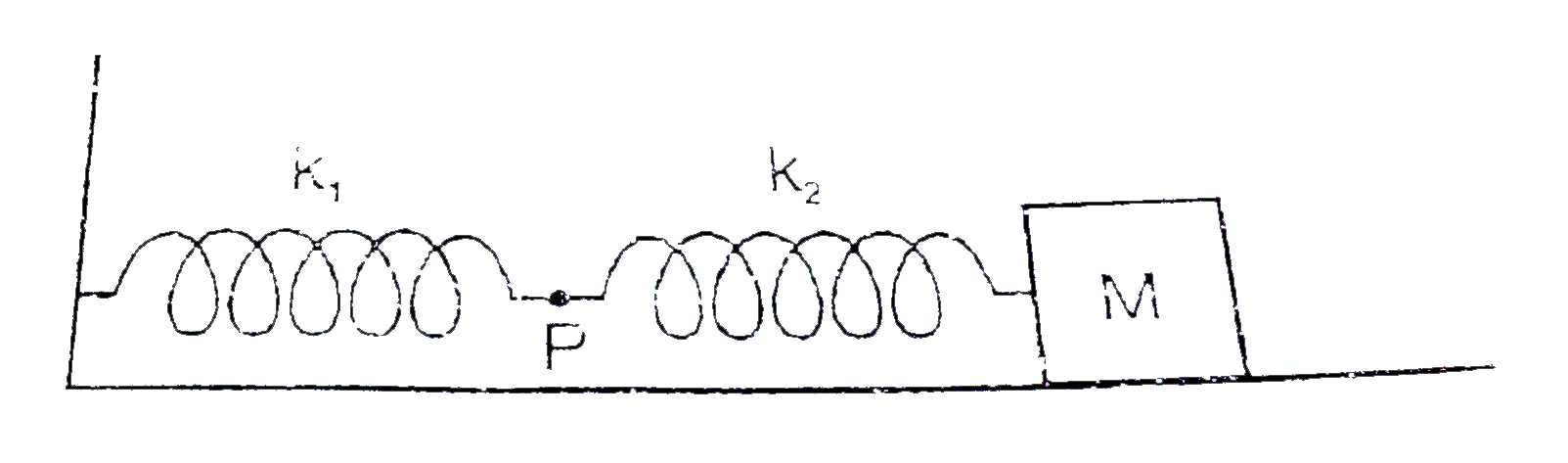B $\frac{k_{2} A}{k_{1}}$
C $\frac{k_{1} A}{k_{1} + k_{2}}$
D $\frac{k_{2} A}{k_{1} + k_{2}}$
Question 3 - Select One
The mass M shown in the figure oscillates in simple harmonic motion with amplitude A. The maximum speed of junction P is $V_{0}$ . Assume springs are massless. Select the correct option/s

AAmplitude of potential energy is springs $S_{1}$ and $S_{2}$ is respectivley $\frac{1}{9} k A^{2}$ and $k A^{2}$
BAmplitude of potential energy is $S_{1}$ and $S_{2}$ is respectively $\frac{2}{9} k A^{2}$ and $\frac{1}{9} k A^{2}$
C $V_{0} = A \sqrt{\frac{8 k}{27 M}}$
D $V_{0} = A \sqrt{\frac{8 k}{81 M}}$

ALLEN-SIMPLE HARMONIC MOTION-Exercise-05 [B]

Home
Ask Doubt
Profile