A particle of mass is confined to a narrow tube of length L.
(a) Find the wavelengths of the de-Brogile wave which will resonate in the tube.
(b) Calculate the corresponding particle moments. and
(c) Calculate the corresponding energies.
(a) The de-Brogile waves will resonate with a node at each end of the tube.
Few of the possible resonance forms are as follows : λn=2Ln,n=1,2,3……..
_S01_014_S01.png)
(b) _S01_014_S02.png) Since d-Broigle wavelengths are λn=hpn
Since d-Broigle wavelengths are λn=hpn
pn=hλn=nh2L,n=1,2,3......... _S01_014_S03.png)
(c) The kinetic energy of the particles are Kn=p2n2m−n2h28L2m,n=1,2,3.....
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Nuclear Physics : Solved Example
5 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Radioactivity : Solved Example
6 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Photo Elertric Effectric : Solved Example
1 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)
25 Videos
- TEST PAPERBOOK - ALLENCHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
Similar Questions
A uniform rod of mass m and length 2L on a smooth horizontal surface. A particle of mass m is connected to a string of length L whose other end is connected to the end ‘A’ of the rod. Initially the string is held taut perpendicular to the rod and the particle is given a velocity v0 parallel to the initial position of the rod.
(a) Calculate the acceleration of the centre of the rod immediately after the particle is projected.
(b) The particle strikes the centre of the rod and sticks to it. Calculate the angular speed of the rod after this.

View SolutionCalculate de-Brogie wavelength of a hydrogen atom with translational energy corresponding to a temperature of 27∘C.
View Solution
Knowledge Check
A material particle with a rest mass mo is moving with a velocity of light c. Then, the wavelength of the de Broglie wave associated with it is
A(hmoc)BzeroC∞D(moch)An electron is confined to a tube of length L. The electron’s potential energy in one half of the tube is zero, while the potential energy in the other half is 10eV. If the electron has a total energy E=15eV, then the ratio of the deBroglie wavelength of the electron in the 10eV region of the tube to that in the other half is -
A1/√3B√3C3D13For a quantum particle in a box, the lowest energy quantum state has 1/2 of the particle de Broglie wave fitting in the box. The next highest state corresponds to
A1/4 de Broglie wavelengthB1/2 de Broglie wavelengthC1 de Broglie wavelengthD2 de Broglie wavelength
(a) A particle is moving three times as fast as an electron. The ratio of the de-Broglie wavelength of the particle to that of the electron is 1.813×10−4. Calculate the particle's mass and identify the particle.
(b) An electron and proton have the same kinetic energy. which of the two will have larger de Broglie wavelength ? Give reason.
View SolutionCalculate the momentum of a particle which has a de Broglie wavelength of 10nm
View SolutionA pillar having square cross section of side length L is fixed on a smooth floor. A particle of mass m is connected to a corner A of the pillar using an inextensible string of length 3.5 L. With the string just taut along the line BA, the particle is given a velocity v perpendicular to the string. The particle slides on the smooth floor and the string wraps around the pillar.
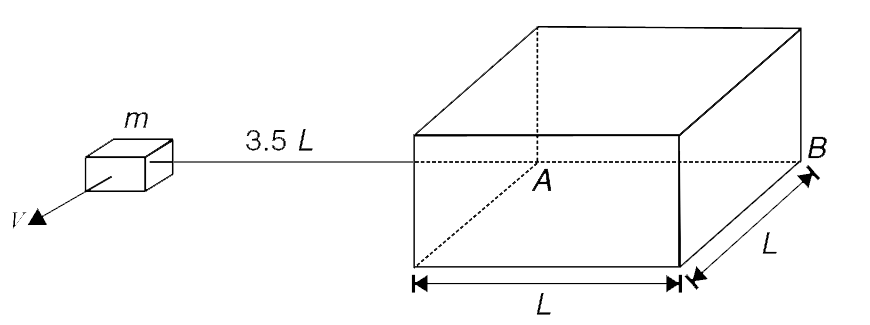
(a) Find the time in which the particle will hit the pillar. (b) Find the tension in the string just before the particle hits the pillar. Neglect any energy loss of the particle.
View SolutionWhat are (a) the energy of a photon corresponding to wavelength 1.00 nm, (b) the kinetic energy of an electron with de Broglie wavelength 1.00 nm, (c) the energy of a photon corresponding to wavelength 1.00 fm, and (d) the kinetic energy of an electron with de Broglie wavelength 1.00 fm?
View SolutionCalculate the momentum of a particle which has de Broglie wavelength of 0.1 nm.
View Solution
