The number of photons (λ=6630Å) that strije per second on a totoally reflecting screen (as shown in figure), so that a force of 1N is exerted on the screen, is approximentely).
_E01_001_Q01.png)
1023
1027
1025
1026
The correct Answer is:B
F=dpdt⇒F=(2PsinθΔt)
⇒F=2nsinθ [n= number of photon]
⇒1N=2[n]hλsin30∘⇒n=1027
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise-0219videos
SIMPLE HARMONIC MOTION
- BOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise- 3 Match The Column1videos
SIMPLE HARMONIC MOTION
- BOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example1videos
SIMPLE HARMONIC MOTION
- BOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)25videos
RACE
- BOOK - ALLENCHAPTER - TEST PAPEREXERCISE - PHYSICS4videos
TEST PAPER
Similar Questions
Two coherent monochromatic point sources S1 and S2 are placed in front of an infinite screen as shown in figure. Wavelength of the light emitted by both the sources is zero. Initial phase difference between the sources is zero.
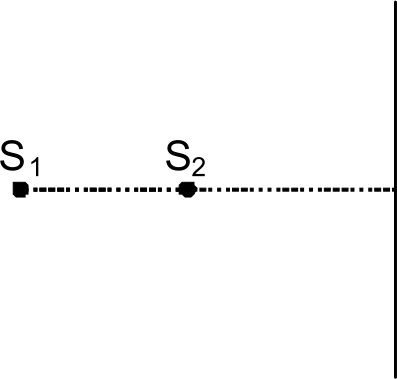
Initially S1S2=2.5λ and the number of bright circular rings on the screen in n1. if the distance S1S2 is increased and made 5.7λ, the number of bright circular rings becomes n2. the difference n2−n1 isView SolutionInterference effects are produced at point P on a screen as a result of direct rays from a 500 nm source and reflected rays from a mirror, as shown in figure. If the sources is 100m to the left of the screen and 1.00 cm above the mirror, find the distance y (in milimeters) to the first dark band above the mirror.
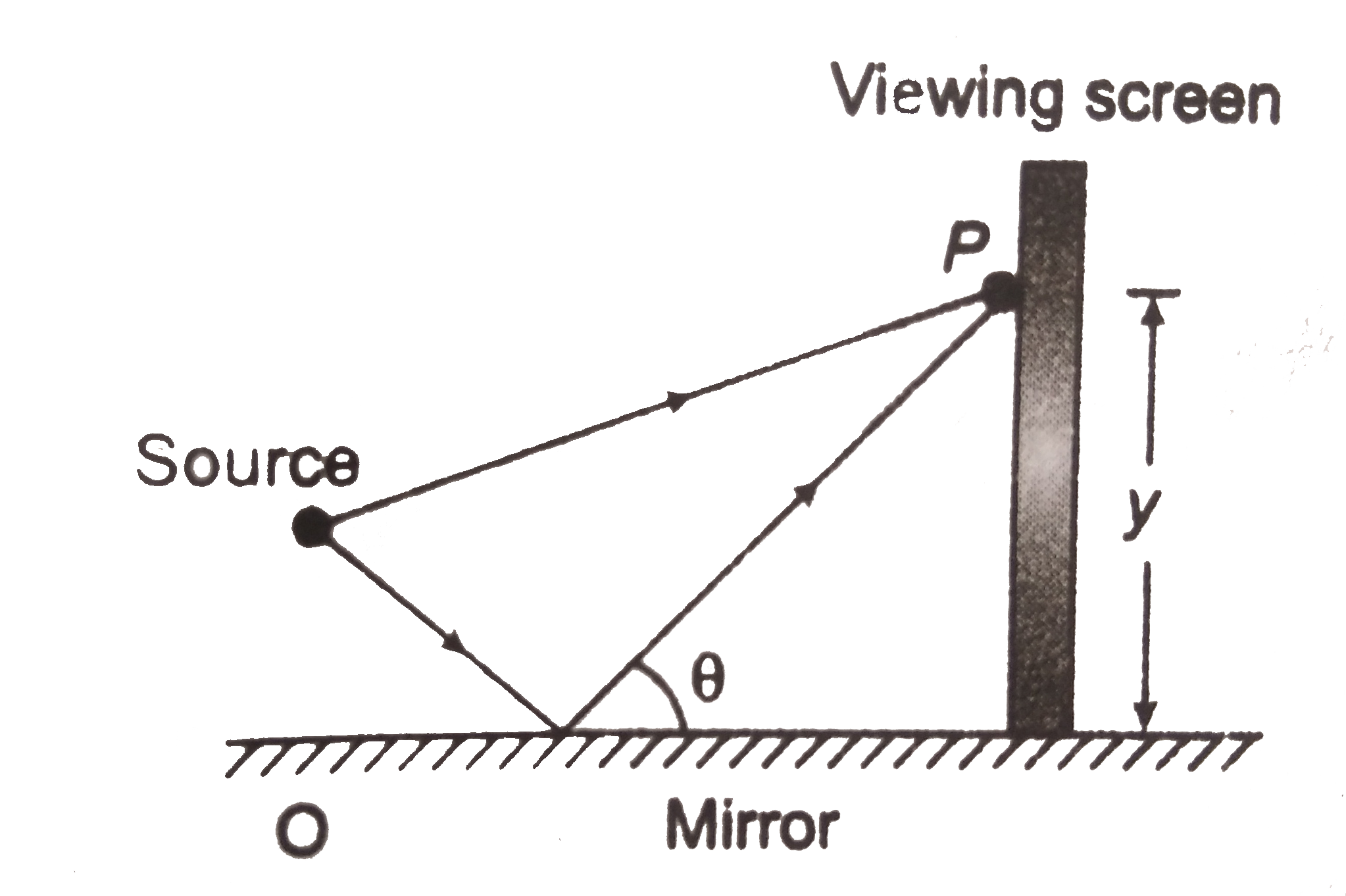
View Solution
Knowledge Check
- Question 1 - Select One
Three coherent point sources S1,S2andS3 are placed on a line perpendicular to the screen as shown in the figure. The wavelength of the light emitted by the sources is lambda. The distance between adjacent sources is d=3λ The distance of S2 from the screen is D(>>λ). Find the minimum (non zero) distance x of a point P on the screen at which complete darkness is obtained.
A2√2D7B√(17)D8C4√5DD4√2D7 - Question 2 - Select One
The energy levels of a hypotherical one electron atom are shown in figure
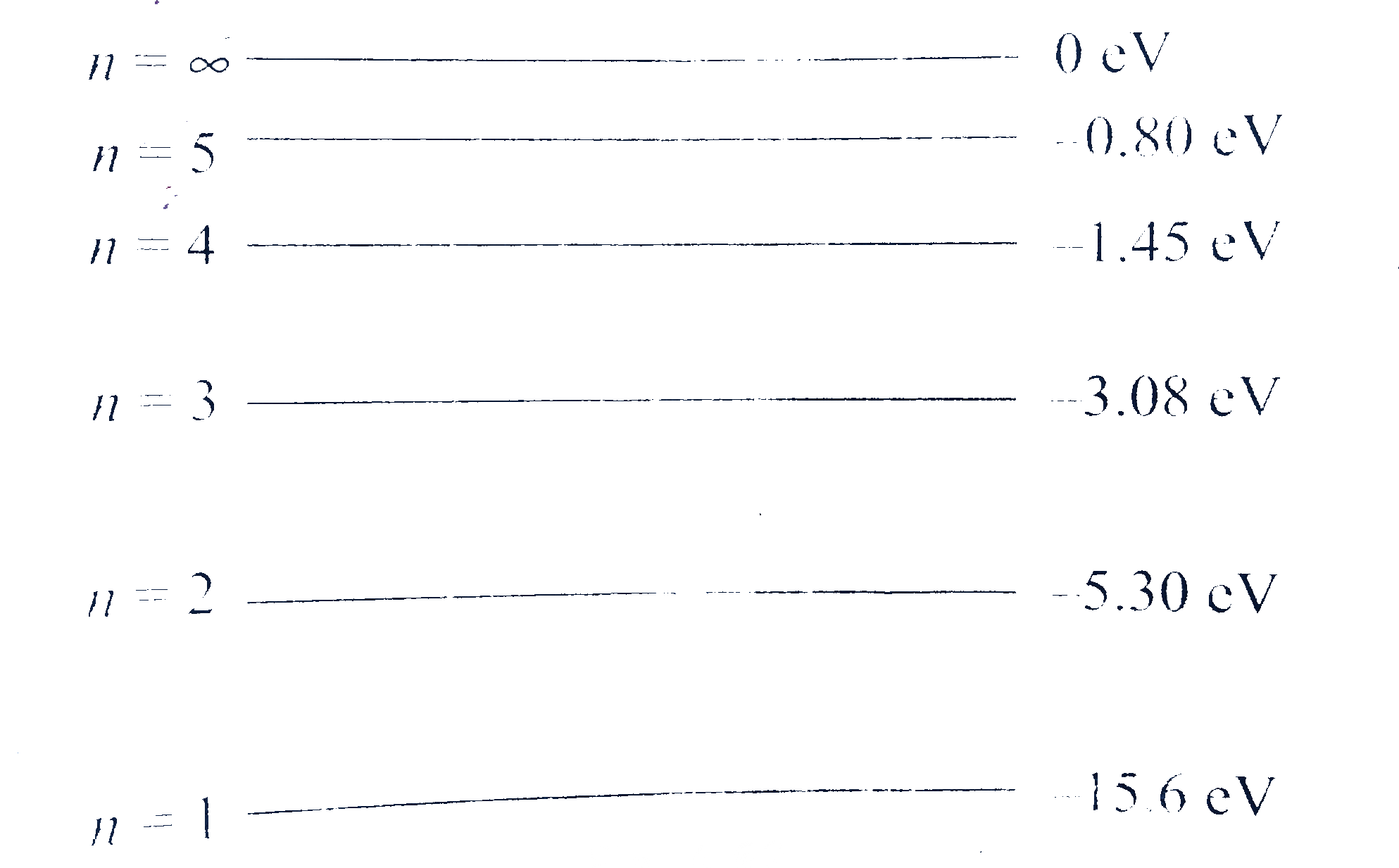
Find the wave number of the photon emitted for the transition n=3→n=1A2.23×107m−1B1.009×107m−1C3.005×106m−1D0.432×106m−1 - Question 3 - Select One
The number of photons falling per second on a completely darkened plate to produce a force of 6.62×10−5N is 'n'. If the wavelength of the light falling is 5×10−7m, then n= __________ ×1022.
(h=6.62×10−34J−s)A1B5C0.2D3.3
Photons of wavelength λ=662 nm are incident normally on a perfectly reflecting screen. Calculate their number per second falling on the screen such that the exerted force is 1 N.
View SolutionFigure. Illustrates the interference axperiment with Fresnel mirrors. The angle between the mirrors is α=12' the distance from the mirrors intersection line to the narrow slit S and the screen Sc are equal to r=10.0cm and b=130cm resoectively. the wavelength of light is λ=0.55μm. Find:
(a) the width of a fringe on the screen and the number of possible maxima,
(b) the shift of the interference pattern on the screen when the slit is displaced by ∂l=1.0mm along the are of radius r with centre at the point O,
(c) at what maximum width ∂max of the slit the interference fringes on the screen are still observed sufficiently sharp.
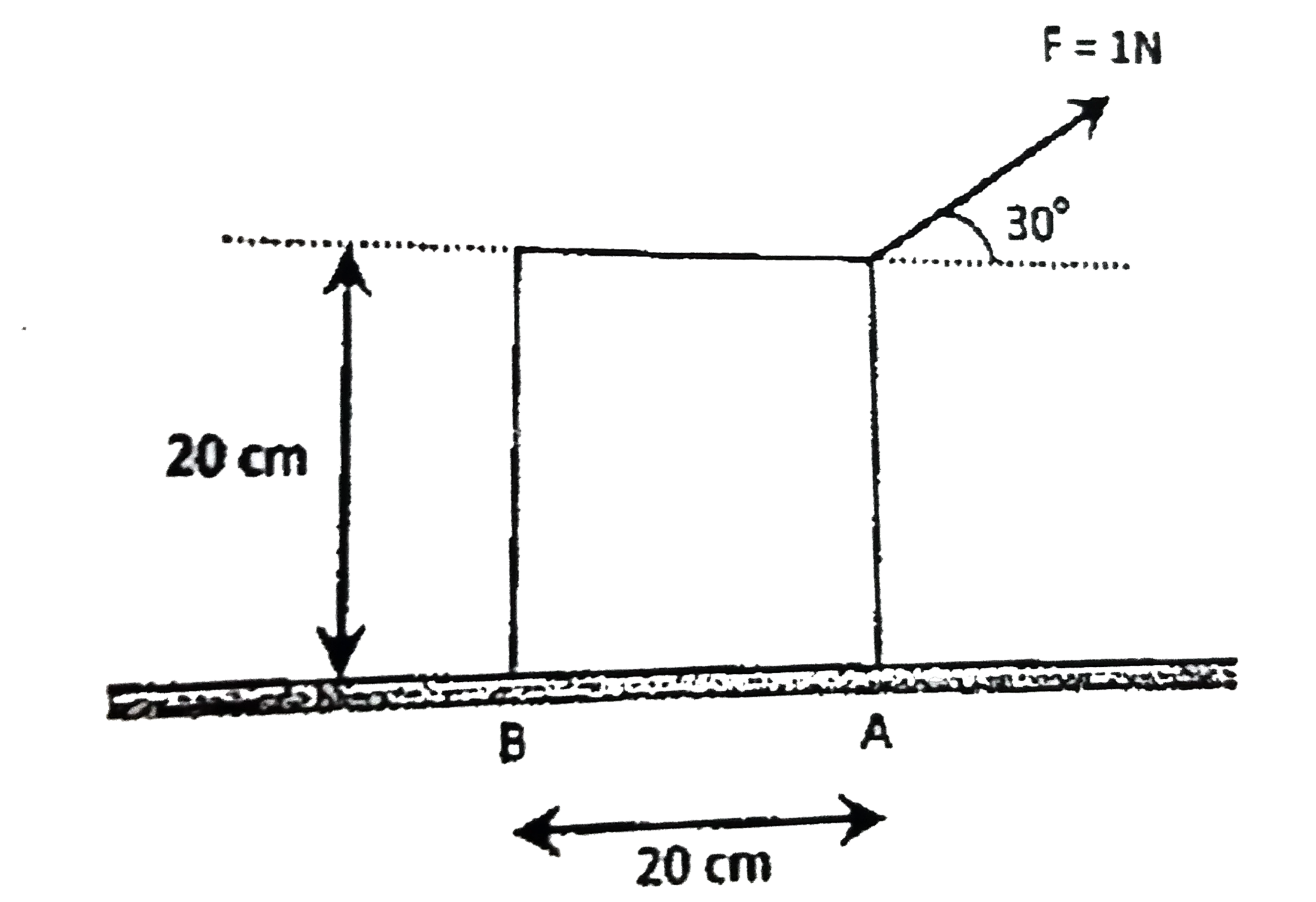
View SolutionA block of mass √3/10kg is placed on a rough horizontal surface as shown in the figure. A force of 1N is applied at one end of the block and the block remains stationary. The normal force exerted by the sruface on the block acts(g=10m/s2)
View SolutionA point sources S emitting light of wavelength 600nm is placed at a very small height h above the flat reflecting surface AB(see figure).The intensity of the reflected light is36% of the intensity.interference firnges are observed on a screen placed parallel to the reflecting surface a very large distance D from it.
(A)What is the shape of the interference fringes on the screen?
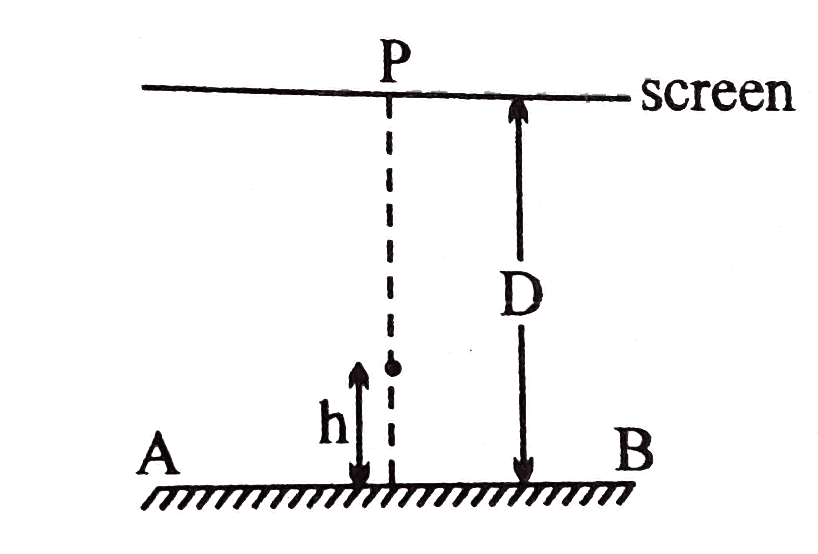
(B)Calculate the ratio of the minimum to the maximum to the maximum intensities in the interference fringes fromed near the point P (shown in the figure) (c) if the intenstities at point P corresponds to a maximum,calculate the minimum distance through which the reflecting surface AB should be shifted so that the intensity at P again becomes maximum.View SolutionA point is emitting light of wavelength 6000Å is placed at a very small height h above a flat reflecting surface MN as shown in the figure.The intensity of the reflected light is 36% of the incident intensity.Interference fringes are observed on a screen placed parallel to the reflecting surface at a very large distance D from it.
If the intensity at pbe maximum then the minimum distance through which the reflecting suface MN should be displaced so that at P again becomes a mixture.?View Solution