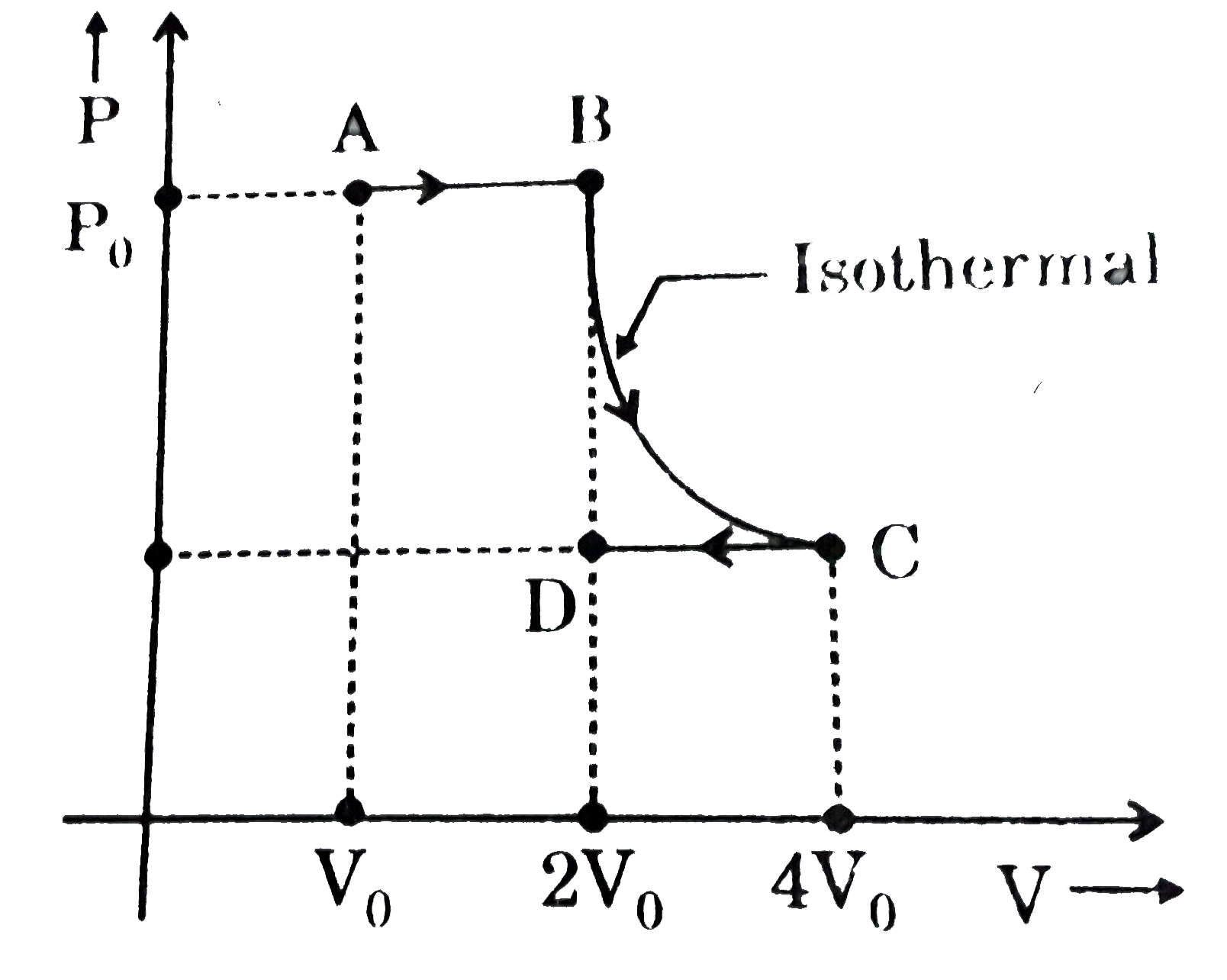
One mole monoatomic ideal gas was taken through process ABCD as show in . Calculate
(i) $W_{A B}, W_{B C}, W_{C D}, W_{D A}$
(ii) $q_{A B}, q_{B C}, q_{C D}, q_{D A}$
(iii) $Δ H_{A B}, Δ H_{B C}, Δ H_{C D}, Δ H_{D A}$
$[U s e : ln (3 / 2) = 0.40 : I n (4 / 3) = 0.29]$

Text Solution

Verified by Experts

(i) $W_{A B}$ : Along 'AB' pressure is variable
from graph : $\frac{V - 10}{T - 300} = \frac{15 - 10}{600 - 300} \Rightarrow 60 V - 600 = T - 300 \Rightarrow 60 V - 300 = T$
sub value of T in ideal gas equation
$P V = R (60 V - 300) \Rightarrow P = 60 R - \frac{300 R}{V}$
$W_{A B} = - 15 \int 10 P d V = - 15 \int 10 [60 R - \frac{300 R}{V}] d V = - 60 R (V_{2} - V_{1}) + 300 R ln (\frac{V_{2}}{V_{1}})$
$= - 300 R + 300 R (0.4) (taken ln (3 / 2) = 0.10 data)$
$W_{A B} = - 180 R = - 1496.52 J$
$W_{B C} = - R T ln (\frac{V_{3}}{V_{2}}) = - R T (4 / 3) (taken ln (4 / 3) = 0.29 data)$
$= - 8.314 \times 600 \times 0.29 = - 1446.63 Joule$
$W_{C D} = 0$
$W_{D A} = - n R T ln (\frac{V_{1}}{V_{2}}) = - 1 \times 8.314 \times 300 ln (\frac{10}{20}) = + 1728.84 Joule$
(ii) $q_{A B} = Δ E_{A B} - W = \frac{3}{2} R \times 300 + 1496.52 = 450 R + 180 R = 630 R = 5237.82 Joule$
$q_{B C} = - W_{B C} = + 1446.63 Joule$
$q_{C D} = Δ U = n C_{V} Δ T = 1 \times \frac{3}{2} R \times (300 - 600) = - 3741.3 Joule$
$q_{D A} = - W_{D A} = 1728.84 Joule$
(iii) $Δ H_{A B} = C_{P} (T_{2} - T_{1}) = \frac{5}{3} R \times 300 = 750 R = 6235.5 Joule$
$Δ H_{B C} = 0$
$Δ H_{C D} = Δ U_{C D} + n R Δ T = n C_{p} Δ T = 1 \times \frac{5}{2} R \times (- 300) = - 6235.5 Joule$
$Δ H_{D A} = Δ U_{D A} + n R Δ T = 0 Joule$

Updated on:21/07/2023