As ideal gas undergoing cyclie process ABC .A consisting of isothermal expansion AB, isobaric compression BC & adiabatic copmression CA. Find the %(approximate) efficiency of cycle.
![As ideal gas undergoing cyclie process ABC .A consisting of isothermal expansion AB, isobaric compression BC & adiabatic copmression CA. Find the %(approximate) efficiency of cycle. [Given : T(A)= T(B)= 400 K , gamma =1.5, In 2= 0.7,2^(1//3)=0.8]](https://d10lpgp6xz60nq.cloudfront.net/physics_images/BSL_CHM_THRM_S01_052_Q01.png)
Topper's Solved these Questions
- THERMODYNAMICSBook:BANSALChapter:THERMODYNAMICSExercise:Exercise
Explore 14 Videos
- THERMODYNAMICSBook:BANSALChapter:THERMODYNAMICSExercise:Exercise 1
Explore 35 Videos
- THERMODYNAMICSBook:BANSALChapter:THERMODYNAMICSExercise:Exercise 3
Explore 43 Videos
- THERMOCHEMISTRYBook:BANSALChapter:THERMOCHEMISTRYExercise:Exercise 4
Explore 15 Videos
Similar Questions
The efficiency of a heat engine is defined as the ratio of the mechanical work done by the engine in one cycle to the heat absorbed from the high temperature source . η=WQ1=Q1−Q2Q1 Cornot devised an ideal engine which is based on a reversible cycle of four operations in succession: isothermal expansion , adiabatic expansion. isothermal compression and adiabatic compression.
_E01_238_Q01.png)
For carnot cycle Q1T1=Q2T2. Thus η=Q1−Q2Q1=T1−T2T1 According to carnot theorem "No irreversible engine can have efficiency greater than carnot reversible engine working between same hot and cold reservoirs"._E01_238_Q02.png)
Efficiency of a carnot's cycle change from 16 to 13 when source temperature is raised by 100K. The temperature of the sink is-
View Solution
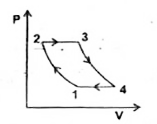
n moles of a monoatomic gas undergoes a cyclic process ABCDA as shown. Process AB is isobaric, process BC is adiabatic process CD is isochoric and process DA is isothermal the maximum temperature and minimum temperature in cycle are 4T0 and T0 respectively. Then:
View Solution
Knowledge Check
The efficiency of a heat engine is defined as the ratio of the mechanical work done by the engine in one cycle to the heat absorbed from the high temperature source . η=WQ1=Q1−Q2Q1 Cornot devised an ideal engine which is based on a reversible cycle of four operations in succession: isothermal expansion , adiabatic expansion. isothermal compression and adiabatic compression.
_E01_237_Q01.png)
For carnot cycle Q1T1=Q2T2. Thus η=Q1−Q2Q1=T1−T2T1 According to carnot theorem "No irreversible engine can have efficiency greater than carnot reversible engine working between same hot and cold reservoirs"._E01_237_Q02.png)
An inventor claims to have developed an engine working between 600K and 300K capable of having an efficiency of 52%, then -AIt is impossibleBIt is possibleCIt is nearly possibleDData is insufficientThe efficiency of a heat engine is defined as the ratio of the mechanical work done by the engine in one cycle to the heat absorbed from the high temperature source . η=WQ1=Q1−Q2Q1 Cornot devised an ideal engine which is based on a reversible cycle of four operations in succession: isothermal expansion , adiabatic expansion. isothermal compression and adiabatic compression.
_E01_238_Q01.png)
For carnot cycle Q1T1=Q2T2. Thus η=Q1−Q2Q1=T1−T2T1 According to carnot theorem "No irreversible engine can have efficiency greater than carnot reversible engine working between same hot and cold reservoirs"._E01_238_Q02.png)
Efficiency of a carnot's cycle change from 16 to 13 when source temperature is raised by 100K. The temperature of the sink is-A10003KB5003KC250KD100K
n moles of a monoatomic gas undergoes a cyclic process ABCDA as shown. Process AB is isobaric, process BC is adiabatic process CD is isochoric and process DA is isothermal the maximum temperature and minimum temperature in cycle are 4T0 and T0 respectively. Then:ATB>TC>TDBheat is released by the gas in the process CDCgeat is supplied by the gas to the surrounding in the process ABDheat is supplied to the gas to the surrounding in the process AB

n moles of a monoatomic gas undergoes a cyclic process ABCDA as shown. Process AB is isobaric, process BC is adiabatic process CD is isochoric and process DA is isothermal the maximum temperature and minimum temperature in cycle are 4T0 and T0 respectively. Then:
View SolutionA gas undergoes cyclic process 1-2-3-4-1 in which 1-2 and 3-4 are adiabatic process 2-3 and 4-1 are isobaric process. If P2P1=k then what will be the efficiency of cycle in terms of k and γ where γ=Cp/Cv.
View SolutionAn ideal gas undergoes a cyclic process as shown. Part of the process ab is isothermal expansion and work done by the gas in this expansion is 700 J. in adiabatic expansion be it again does 400 J work. If it rejects 100 J heat when it returns to a from c via b' then find efficiency of the cycle.
View SolutionAn ideal gas undergoes a cyclic process as shown. Part of the process ab is isothermal expansion and work done by the gas in this expansion is 700 J. in adiabatic expansion be it again does 400 J work. If it rejects 100 J heat when it returns to a from c via b then find efficiency of the cycle.
View SolutionOne mole of a diatomic ideal gas (γ=1.4) is taken through a cyclic process starting from point A. The process A→B is an adiabatic compression, B→C is isobaric expansion, C→D is an adiabatic expansion, and D→A is isochoric. The volume ratios are VA/VB=16andVC/VB=2 and the temperature at A is TA=300K. Calculate the temperature of the gas at the points B and D and find the efficiency of the cycle.
View Solution
