Assume ideal gas behaviour for all the gas considered & vibrational degrees of freedom to be active.
Separated equimolar sample of He,H2,SO2&CH4 were subjected to a two step process as mentioned.
Initially all are at same state of tempreature & prssure.
Step-I → All undergo reversible adiabatic expansion to attain same final volume, which is
double the original volume thereby causing the decreases in their temperature .
Step -II → After step I all are given appropriate amount of heat isochorically to restore the
Mark the correct option(s).
Due to step -I only, the decrease in the tempreature will be maximum for CH4
During step II, heat given will be maximum for CH4
There will be no change in internal energy for any of the gas after both the steps of process are completed.
The P-V graph of CH4 & SO2 will be same.
The correct Answer is:B, C
∵ Ideal gas & initial & final temperature are same
∵DelatE=0 for all
∵ (C) is correct
Also ∵|W| is maximum for CH4 is step I & overall
ΔE=0∵|q| for CH4 will be maximum
∵ option (B) is correct
Since after step I, all have same volume , same moles & pressure of CH4 is highest ∵ Temperature of
CH4 will be highest & since initial it is same
∵ decrease in temperature will be least
∵ option (A) is incorrect
∵γ for the SO2 & CH4 is different (due to vibrational degree of freedom )
∵ graph is different
∵ option (D) is incorrect
∵ option (B), (C)

Topper's Solved these Questions
Similar Questions
Assume ideal gas behaviour for all the gases considered and neglect vibrational degrees of freedom. Separate equimolar sample. Separate equimolar samples of Ne, O2 , CO2 and SO2 were subjected to a two process as mentioned. Initially all are at same state of temperature and pressue.
Step I → All undergo reversible adiabatic expansion to attain same final volume, which is double the original volume thereby causing the decreases in their temperature.
Step II → After step I all are given appropriate amount of heat isochorically to restore the original temperature.
Mark the correct option(s) :
View SolutionIf separate samples of argon, methane, nitrogen and ammonia, all at the same initial temperature and pressure and expanded adiabatically to double their original volumes, then which one of these gases will require the greatest quantity of heat to restore the original temperature?
View Solution
Knowledge Check
Assume ideal gas behavior for all the gases considered and vibratonal degree of freedom to be active. Separated equimolar sample of Ne,O2,So2andCH4 were subjedted to a two step process as mentioned . Initiallyt all are at same state of temperture and pressure.
Step -I: All undergo reversible abiabatic expansion to attain same final volume thereby causing the decreasae in their temperature.
Step -II : After step I, all are given appropriate amount of heat isochorically to restore the original temperature .
Mark the correct optoin(s).ADue to step I only , the decrease in temperature will be maximum for Ne.BDuring step II , heat given will be minimum for CH4CThere will be no net change in internal energy for any of the gas after both the steps of process are completed.DThe (∘)P−V graph of CH4 and SO2 wll be same for overall process.Value of γ for CH4 molecule is (Consider vibarational degree of freedom to be active).
A4/3B1312C1514D1715The degrees of freedom of a triatomic gas is
A6B4C2D8
Mention the degree of freedom for diatomic gas molecules without vibration.
View SolutionMention two factors on which the degrees of freedom of a gas depends.
View SolutionOne mole of an ideal gas is subjected to a two step reversible process A-B and B-C. The volume at A and C is same. Find the value of the ratio
Pressure of gas at CPressure of gas at A
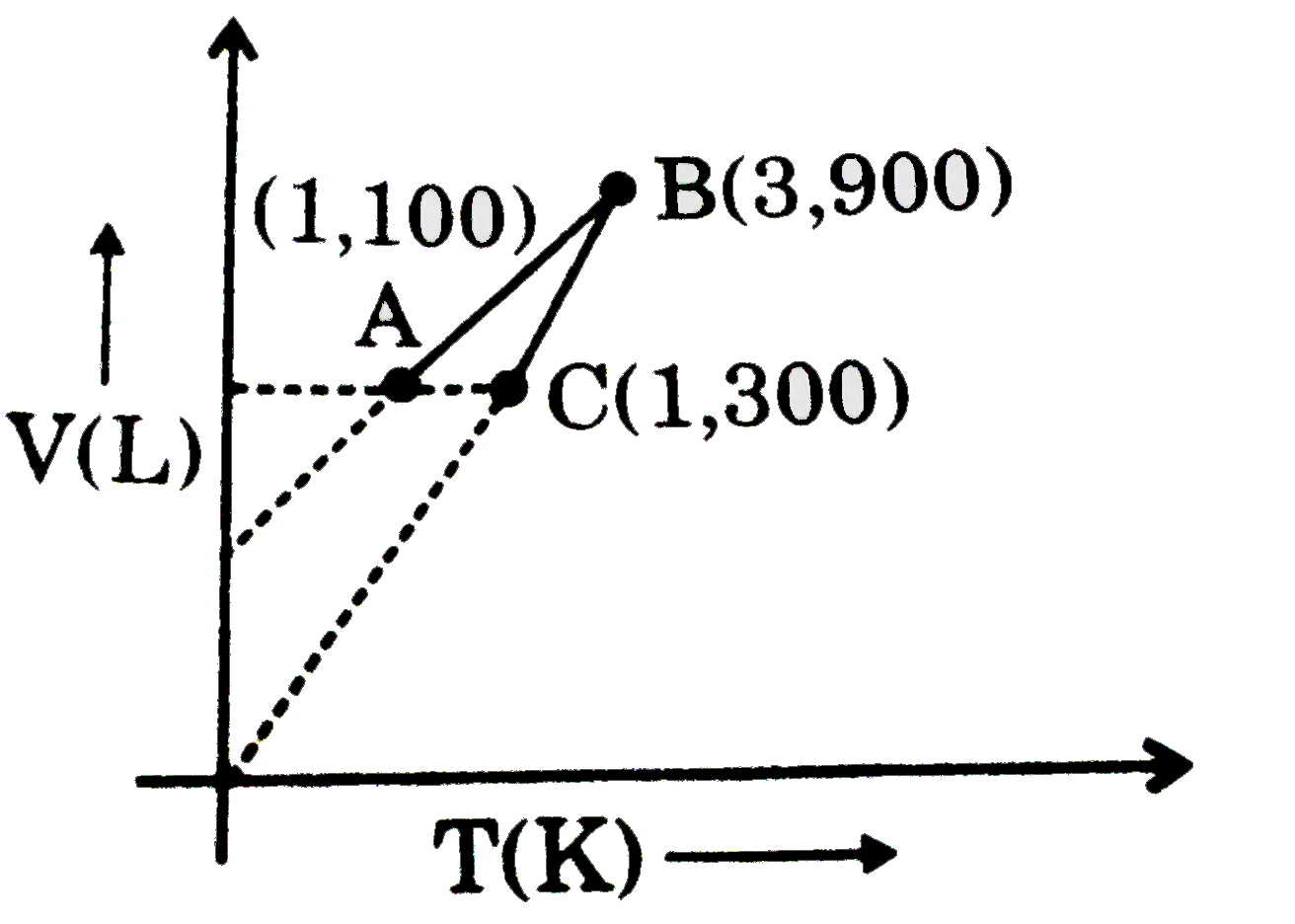
View SolutionA sample of ideal gas is taken through the cyclic process shown in the figure. The temerauture of the gas in state A is TA =200 K. In states B and C the temperature of the gas is the same.
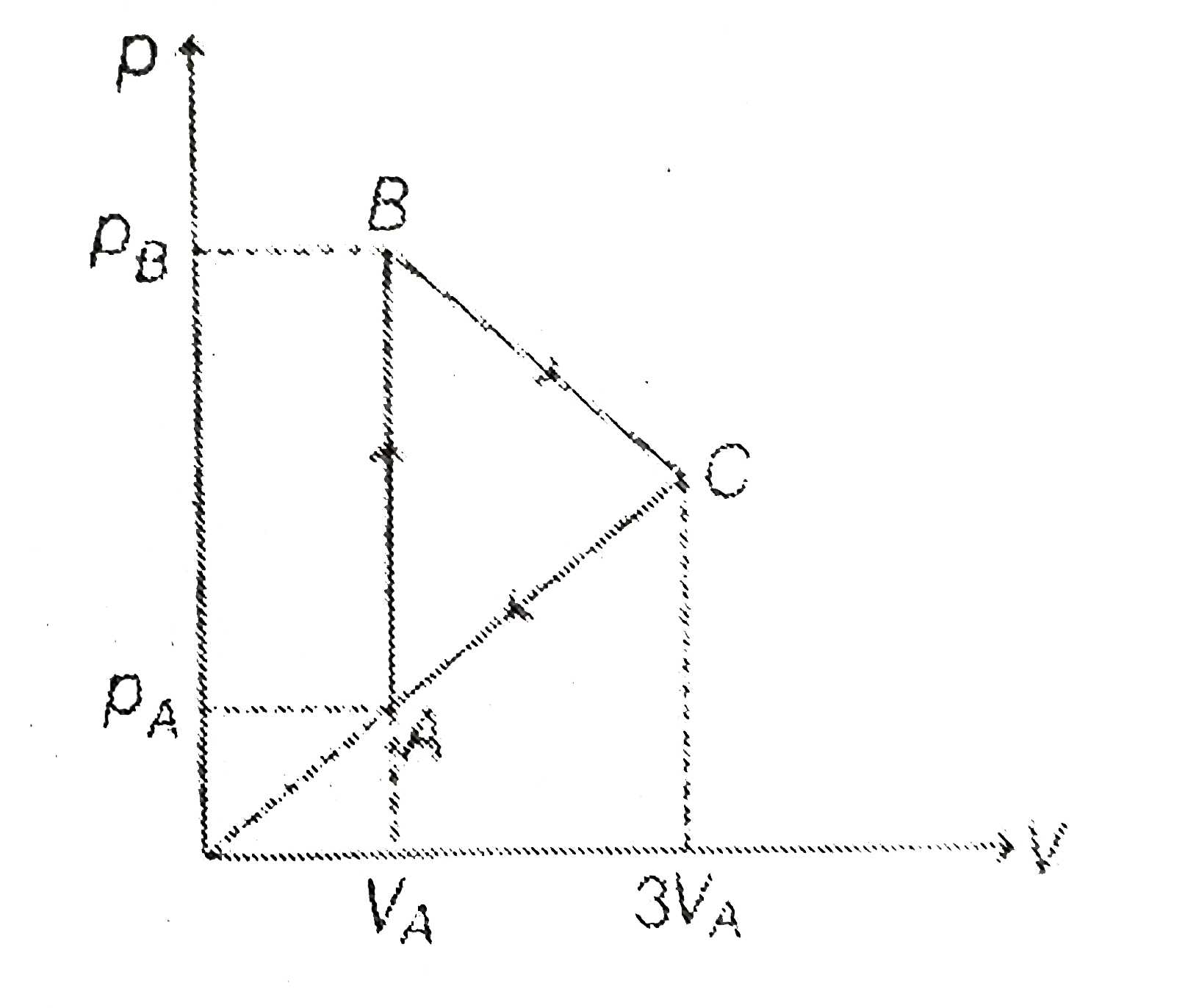
Net work done by the gas in the process is
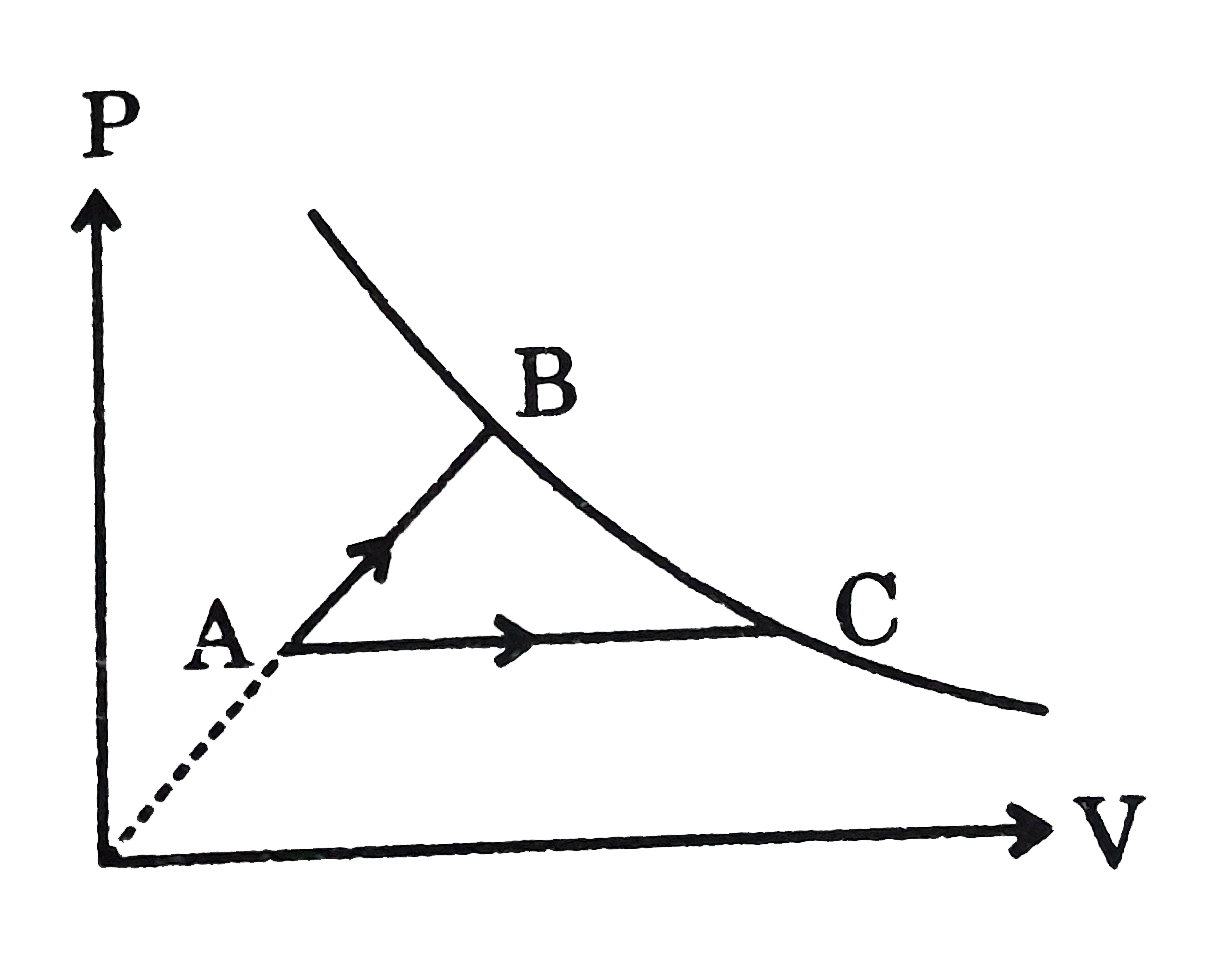
View SolutionAn ideal gas is subjected to two different process in which it is heated to same final temperature from same initial state (A) as shown in diagram, then :
View Solution
