A block B starts sliding down from the point A on a rough wedge. The angle that the incline plane makes with the horizontal is variable having value π3 at A and 0 at B. Also the magnitude of rate of change of θ with x is 2 where x is the length measured along the incline plane starting from A. Assume total length of incline plane to be π6m. Based upon the above situation, answer the following question. (x≥π24m)
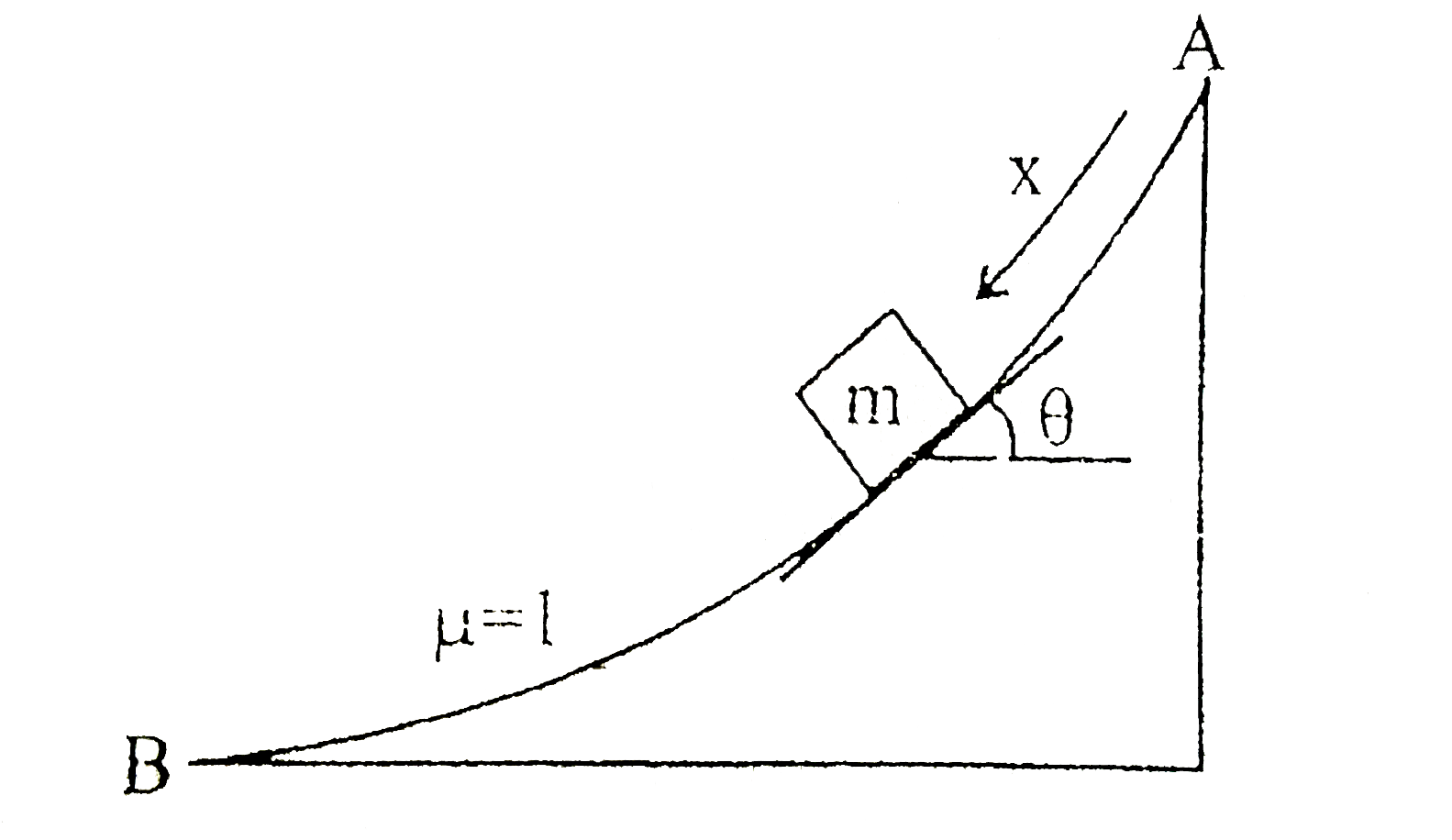
Find x in metre such that the block is in equilibrium over ther
π6
π12
π24
13π24
The correct Answer is:C
dθdx=−2
Δθ=−2Δx
θ−π3=−2[x−0]
θ=−2x+π3
mgsinθ=μmgcosθ (at equilibrium) tanθ=μ
tan(π3−2x)=μ=1
π3−2x=nπ+π4
2x=π12−nπ
x=π24−nπ2
x=...π24−π,π24−π2,π24,π24+π2,π24+π, ....
as x>π24
so, x=π24,π2+π24,π+π24,3π2+π24 .....
Also, θ≥0
so, π3−2x≥0
x≤π6m
so, x=π24m
Topper's Solved these Questions
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (B)
3 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (C )
15 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS
866 Videos
- SEMICONDUCTORSBOOK - BANSALCHAPTER - SEMICONDUCTORSEXERCISE - CBSE Question
32 Videos
Similar Questions
Knowledge Check
A block B starts sliding down from the point A on a rough wedge. The angle that the incline plane makes with the horizontal is variable having value π3 at A and 0 at B. Also the magnitude of rate of change of θ with x is 2 where x is the length measured along the incline plane starting from A. Assume total length of incline plane to be π6m. Based upon the above situation, answer the following question. (x≥π24m)
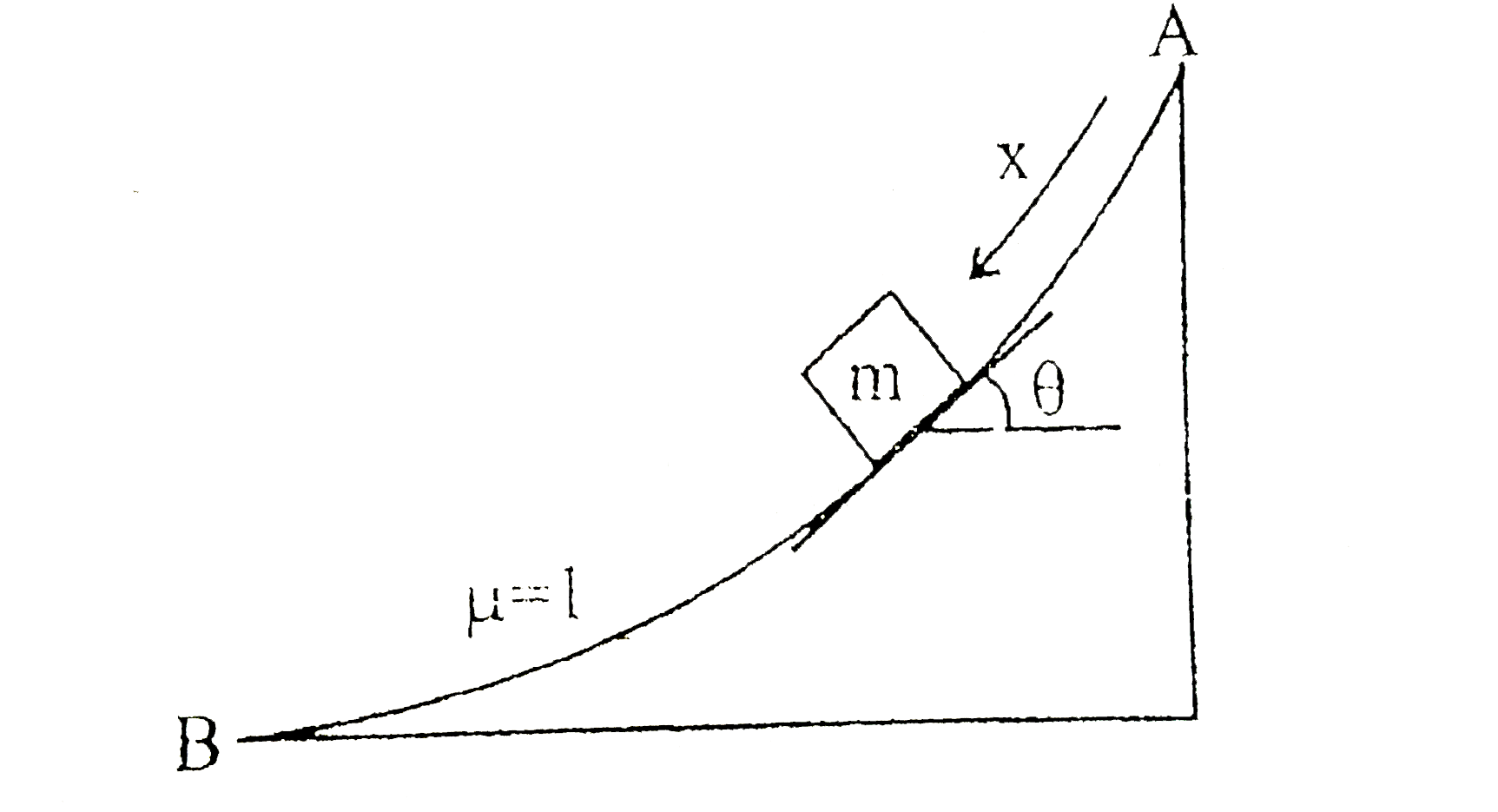
Find velocity of the block as it reaches down at the point B.A5m/sB(5+5√3)m/sC√5−5√3m/sDBlock will not reach at point BThe angle which the rough inclined plane makes with the horizontal when the body placed on it just starts sliding down is called
Aangle of FrictionBangle of reposeCcritical angleDbrewster's angleThe angle which the rough inclined plane makes with the horizontal when the body placed on it just starts sliding down is called .
Aangle of FrictionBangle of reposeCcritical angleDbrewster's angle
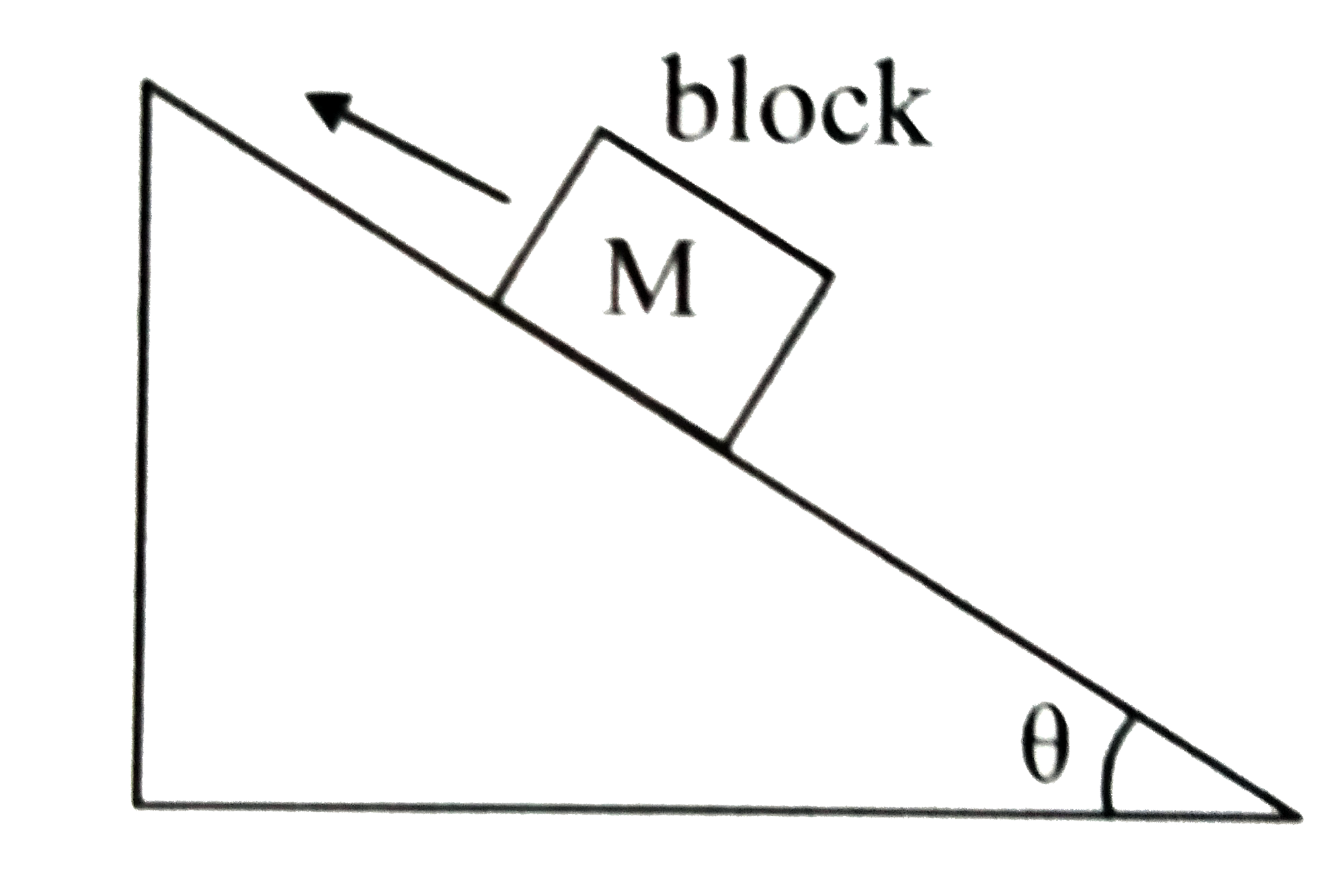
A block of mas M is resting on an inclined plane as shown in the figure. The inclination of the plane to the horizontal is gradually increased. It is found that when the angle of inclination is θ the block just begins to slide down the plane. What is the minimum force F applied parallel to the plane that would just make the block move up the plane ?
View SolutionA block of mass m is sliding down an inclined plane with uniform velocity v. Angle that the plane makes with the horizontal is θ. Assume edge of the cube to be a, calculate torque of the normal reaction about the centre of the block.
View SolutionA block of mass m is placed on a smooth inclined plane of inclination θ with the horizontal. The force exerted by the plane on the block has a magnitude
View SolutionA block of mass 'M' is slipping down on a rough inclined of inclination α with horizontal with a constant velocity. The magnitude and direction of total reaction from the inclined plane on the block is :
View SolutionOn an inclined plane two particles AandB are projected with same speed at the same angle with the horizontal, particle A down and particle B up the plane. If the ratio of time of flight of AandB is cotθ, where θ is the angle at which B is projected measured from inclined plane, find the angle at which particles are projected.
View Solution

