To make the central fringe at the centerO , mica sheet of refractive index 1.5 is introduced Choose the corect statement.
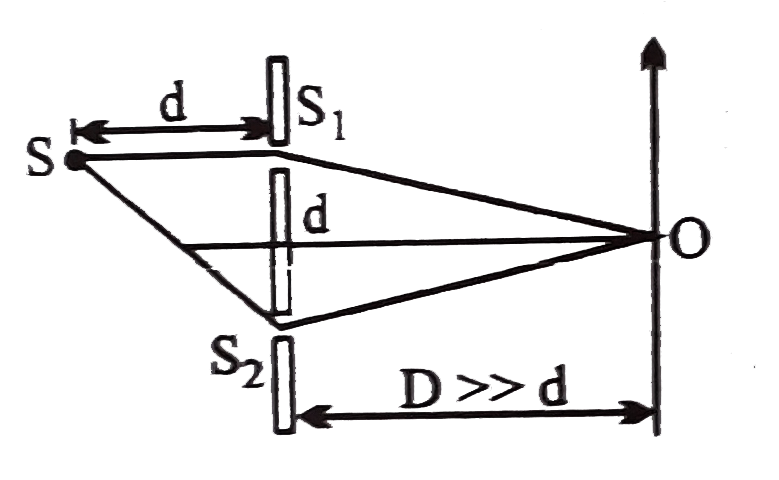
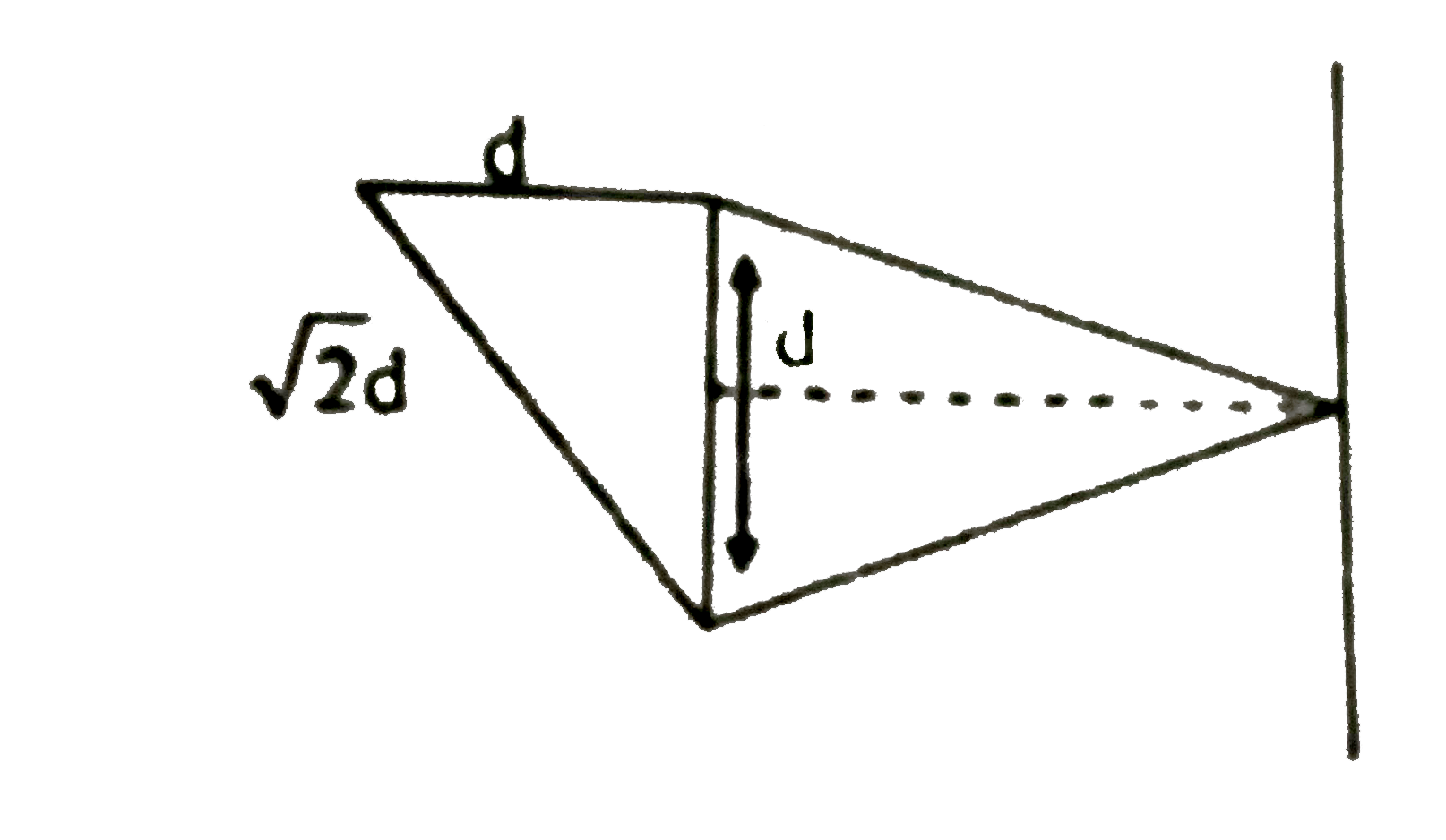
The thickness of sheet is 2(√2−1)d in front of S1
The thickness of sheet is (√2+1)d in front of S2
The thickness of sheet is (2√2d−1) in front of S2
The thickness of sheet is (2√2−1)d in front of S1
The correct Answer is:A
√2d−d=(μ−1)t⇒t=2(√2−1)d
Topper's Solved these Questions
Similar Questions
In YDSE using monochromatic light, the fringe pattern shifts by a certain distance on the screen when a mica sheet of refractive index 1.5 and thickness 2 microns is introduced in the path of one of the interfering waves. The mica sheet is then removed and the distance between the plane of slits and the screen is doubled. It is found that the distance between successive maxima (or minima) now is the same as the observed fringe shift upon the introduction of the mica sheet. Calculate the wavelength of the light.
View SolutionIn YDSE, the central bright fringe produced by light of wavelength 5600Å shifts to the position of 5th bright fringe when a thin transparent film of refractive index 1.28 is introduced in the path of light from one of the two slits. Find the thickness of the film.
View Solution
Knowledge Check
The central fringe of the interference pattern produced by the light of wavelength 6000 Å is found to shift to the position of 4th dark fringe after a glass sheet of refractive index 1.5 is introduced. The thickness of glass sheet would be
A4.8μmB4.2μmC5.4μmD3.0μmThe central fringe shifts to the position of fifth bright fringe, if a thin film of refractive index 1.5 is introduced in the path of light of wavelength 5000Å. The thickness of the glass plate is
A1μmB5μmC3μmD4μmIn Young's experiment using monochromatic light , the fringe pattern shifts by a certain distance on the screen when a mica sheet of refractive index 1.6 and thickness 2 micron is introduced in the path of one of the interfering waves. The
mica sheet is then removed and the distance between the slits and the screen is doubled. it is found that the distance between successive maxima now is the same as the observed fringe shift upon the introduction of the mica sheet . The wavelength of light isA5762ÅB5825ÅC6000ÅD6500Å
In young,s double slit experience monochromatic light, the frings pattern shifts by a certain distance on the screen when a mica sheet of refractive index 1.6 and thickness 1.964 microns is introduced in the path of one of the interfering waves. The mica sheet is then sheet is then removed and the distance between the slits and the screen is doubled. It is found that now the distance between succesive maximum (or minimum) is the same as the observed fringe-shift upon the introduction o fthe mica sheet. Calculate the wavelength of the monochromatic light used in the experiment.
View SolutionIn a Young's double slit experiment using monochromatic light, the fringe pattern shifts by a certain distance on the screen when a mica sheet of refractive index 1.6 and thickness 1.964 microns is introduced in the path of one of the interfering waves. The mica sheet is then removed and the distance between the slits and screen is doubled. It is found that the distance between successive maxima now is the same as observed fringe shift upon the introduced of the mica sheet . Calculate the wavelength of the monochromatic light used in the experiment .
View SolutionIn YDSE using monochromatic light the fringe pattern shifts by a certain distance on the screen when a mica sheet of refractive index 1.6 and thickness 1.964 microns is introduced in the path of one of the interfering waves. The mica sheet is then removed and the distance between the plane of slits and the screen is doubled. It is found that the distance between successive maxima (or minima) now is the same as the observed fringe shift upon the introduction of the mica sheet. Calculate the wavelength of the light.
View SolutionThe refractive index of glass is 1.5. What is meant by this statement ?
View SolutionIn Young's double slit experiment, the fringes are displaced by a distance x when a glass plate of one refractive index 1.5 is introduced in the path of one of the beams. When this plate in replaced by another plate of the same thickness, the shift of fringes is (3/2)x. The refractive index of the second plate is
View Solution
