A cow is tied to a corner (vertex) of a regular hexagonal fenced area of side a metres by a rope of length 5a/2 metres in a grass field. (The cow cannot graze inside the fenced area.) What is the maximum possible area of the grass field to which the cow has access to graze ?
5πa2
52πa2
6πa2
3πa2
The correct Answer is:A
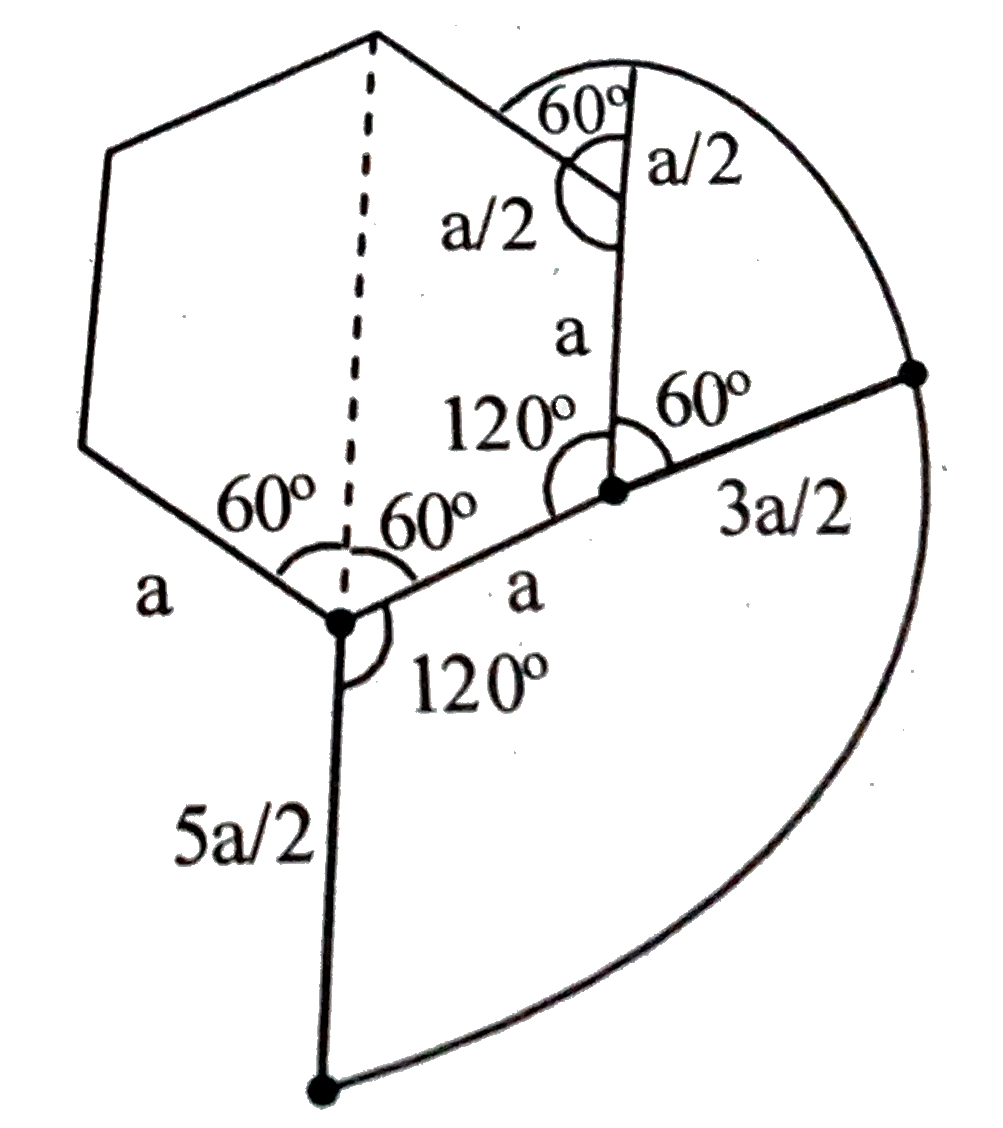
Area=2[120360×π(5a2)2+60360×π(3a2)2+60360×π(a2)2]
=2π3[25a24+9a28+a28]
=2π3×30a24=5πa2
Topper's Solved these Questions
Similar Questions
A horse is tethered to a corner of a rectangular field 80 m by 50 m by a rope of length 7 m . Find the area over which it can graze . Also find the area beyond his reach .
View SolutionA horse is tethered to one corner of a rectangular field of dimensions 70 m × 52 m, by a rope of length 21 m. How much area of the field can it graze?
View Solution
Knowledge Check
- Question 1 - Select One
At each corner of a triangular field of sides 26 m, 28 m and 30 m, a cow is tethered by a rope of, length 7 m. The area (in m2) ungrazed by the cows is
A336B259C154D77 - Question 2 - Select One
At each corner of a triangular field of sides 26m, 28m and 30m, a cow is tethered by a rope of length 7m. The area (in m2) ungrazed by the cows is
A336B259C154D77 - Question 3 - Select One
A cow is tied on the corner of a rectangular field of size 30m×20m by a 14m long rope. The area of the region, that she can graze is (use π=227) :
A350m2B196m2C154m2D22m2
A cow is tied with a rope of length 7 cm at the corncr of a triangular field with cach side 15 an. If the length of the rope is increased by 4.5 m, find increase in area of the field in which the cow can graze.
View SolutionA cow is tied with a rope of length 14m at the corner of a rectangular field of dimensions 20m×16m . Find the area of the field in which the cow can graze.
View SolutionA horse is tied to a peg at one corner of a square shaped grass field of side 15 m by means of a 5 m long rope. Find(i) the area of that part of the field in which the horse can graze.(ii) the increase in the grazing area if the rope were 10 m long instead of 5 m.
View SolutionA horse is tethered to a pole with a 14 metre long rope at the corner of a 40 metre long and 24 metre wide rectangular grass-field. What area of the field will the horse graze?
View SolutionA rectangle field is half as wide as it is long and is completely enclosed by x metre of fencing. What is the area of the field ?
View Solution

