Find the area of the region bounded by the curve y2=9x and y=3x.
Video Solution
Text Solution
The correct Answer is:N/a
We, have y29x and y=3x
→(3x)2=9x
⇒9x2−9x=0
⇒9x(x−1)=0
⇒x=1,0
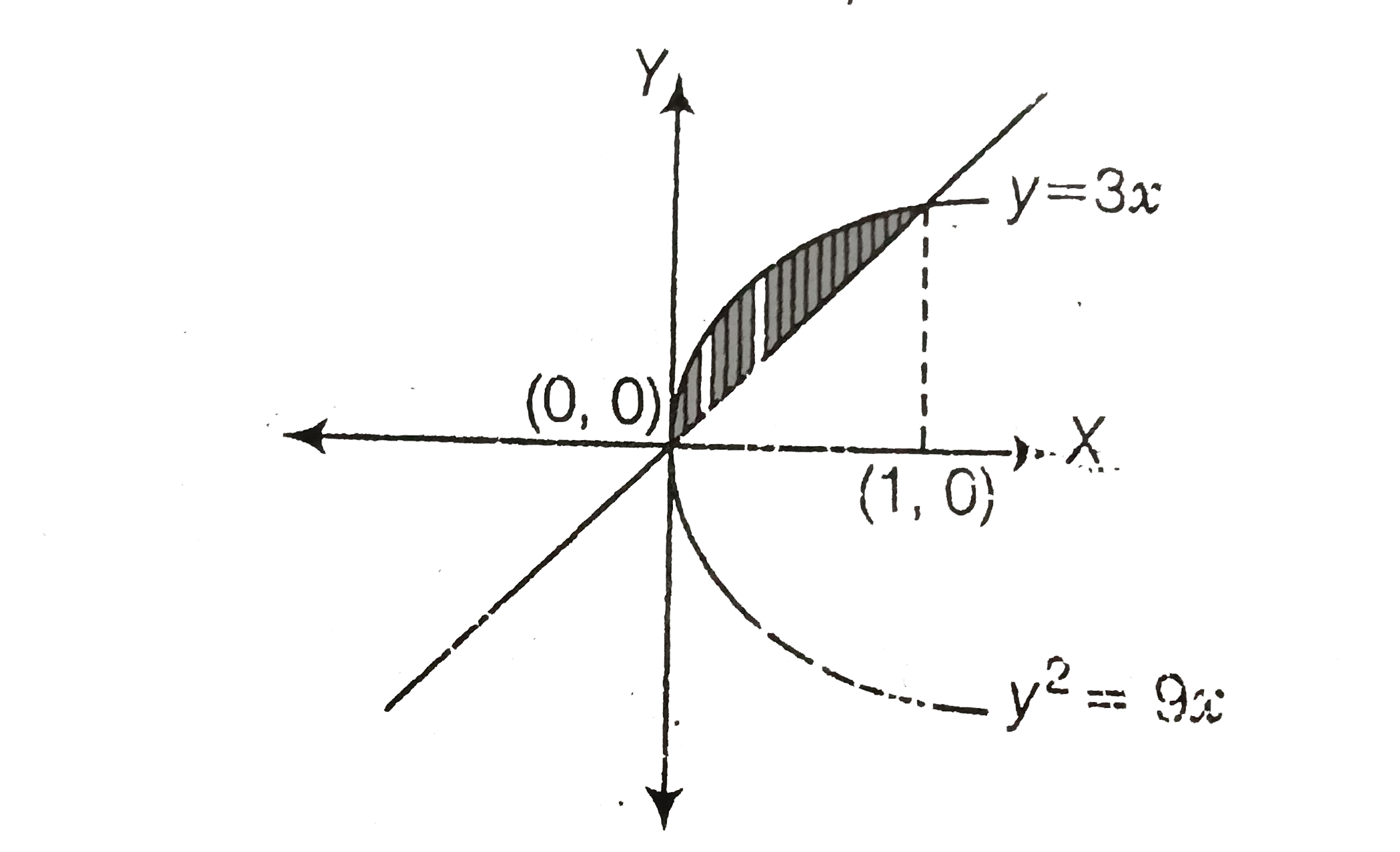
∴Required area, A=∫10√9xcx−∫103xdx
=3∫10x1/2dx−3∫10xdx
=3[x3/23/2]10−3[x22]10
=3(23−0)−3(12−0)
=2−32=12 sq units
|
Updated on:21/07/2023
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
Find the area of the region bounded by the curve y2=4x and x2=4y.
A157 sq unitsB167 sq unitsC163 sq unitsD16 sq units - Question 2 - Select One
Find the area of the region bounded by the curves y2=x+1 and y2=−x+1.
A53 sq. units.B73 sq. units.C83 sq. units.D103 sq. units.
Find the area of the region bounded by the curve y2=2x and x2+y2=4x.
View SolutionFind the area of the region bounded by the curve y2=2x and x2+y2=4x.
View SolutionFind the area of the region bounded by the curve y=x3,y=x+6 and x=0
View SolutionExamples: Find the area of the region bounded by the curve y2=2y−x and the y-axis.
View SolutionFind the area of the region bounded by the curves x=2y−y2 and y=2+x.
View SolutionFind the area of the region bounded by the curves y2=4ax and x2=4ay.
View Solution

