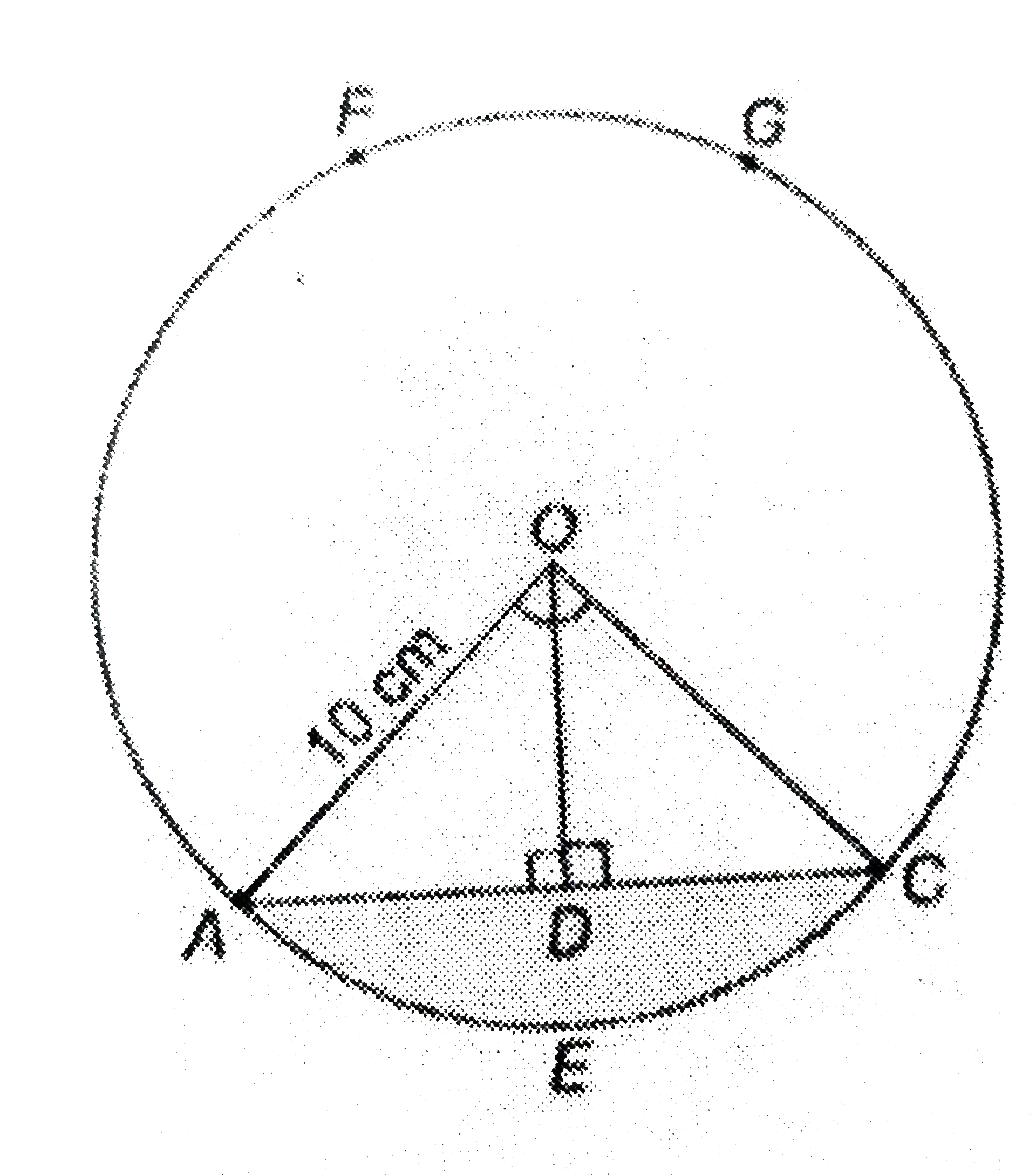
A chord of a circle of radius 10 cm subtends a right angle at the centre. Find the area of the corresponding : (i) minor segment (ii) major sector.

Video Solution

Text Solution

Verified by Experts

given, radius of a circle AO = 10 cm
A kperpendicular is drawn from centre of circle to the chord of the circle, which bisects the chord
$∴ A D = D C$
Alos, $∠ A O D = ∠ C O D = 45^{\circ}$
$∴ A n g \leq A O C = ∠ A O D + ∠ C O D$
$= 45^{\circ} + 45^{\circ} = 90^{\circ}$
In right $Δ A O D$ ,
${sin 45}^{\circ} = \frac{A D}{A O} \Rightarrow \frac{1}{\sqrt{2}} = \frac{A D}{10}$
$\Rightarrow A D = 5 \sqrt{2} c m$
$\Rightarrow A D = 5 \sqrt{2} c m$
and $cos t 45^{\circ} = \frac{O D}{A O} \Rightarrow \frac{1}{\sqrt{2}} = \frac{O D}{10}$
$\Rightarrow O D = 5 \sqrt{2} c m$
Now, $A C = 2 A D$
$= 2 \times 5 \sqrt{2} = 10 \sqrt{2} c m$
Now, area of $Δ A O C = \frac{1}{2} A C \times O D = \frac{1}{2} \times 10 \sqrt{2} \times 5 \sqrt{2} = 50 c m^{2}$
Now, area of sector $= \frac{θ π r^{2}}{360^{\circ}} = \frac{90^{\circ}}{360^{\circ}} \times 3.14 \times {(10)}^{2} = \frac{314}{4} = 78.5 c m^{2}$
(i) $∴$ Area of minor segment $A E C =$ Area of sector OAEC - area of $Δ A O C$
(ii) $∴$ Area of major sector OAFGCO = Area of circle - area of sector OAEC
$= π r^{2} - 78.5 = 3.14 \times {(10)}^{2} - 78.5$
$= 314 - 78.5 = 235.5 c m^{2}$

Updated on:21/07/2023

A chord of circle of a radius 28 cm subtends a right angle at the centre. What is the area of the minor sector?
A $621 c m^{2}$
B $616 c m^{2}$
C $718 c m^{2}$
D $721 c m^{2}$
A chord of a circle of radius $10 c m$ subtends a right angle at the centre. The area of the minor segments (given $π = 3.14)$ is
A $32.5 c m^{2}$
B $34.5 c m^{2}$
C $28.5 c m^{2}$
D $30.5 c m^{2}$