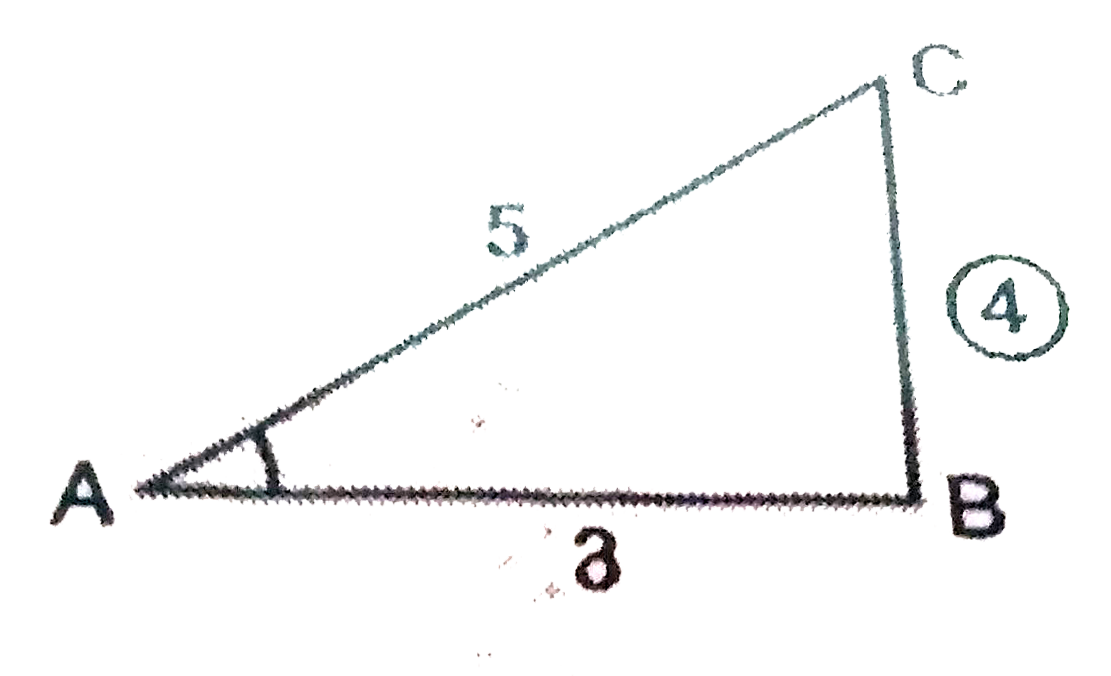
In a $Δ A B C$ the value of $∠ A$ is given by 5 CosA - 3 = 0 then the equation whose roots are sinA and tanA is :

Video Solution

Text Solution

Verified by Experts

We have,
$5 cos A - 3 = 0 \Rightarrow cos A = \frac{3}{5} = \frac{base}{hypotenuse}$
So $∠ A$ must be acute, Now make a base AB such that $∠ B = 90^{\circ}$ and find the perpendicular by Pythagoras theorem.
$∴ sin A \frac{4}{5} and tan A = \frac{4}{3}$
:. Quadratic equation whose roots are sin A and tan A, are
$x^{2} - (sin A + t e n A) x + (sin A . t e n A) = 0 (:' equation is x^{2} - S . x + P = 0)$
$\Rightarrow x^{2} - (\frac{4}{5} + \frac{4}{3}) x + (\frac{4}{5} \times \frac{4}{3}) = 0$
$\Rightarrow x^{2} - (\frac{12 + 20}{15}) x + \frac{16}{15} = 0$
$\Rightarrow 15 x^{2} - 32 x + 16 = 0$

Updated on:21/07/2023

If $α, β$ are the roots of the equation $x^{2} - 3 x + 5 = 0$
and $γ, δ$ are the roots of the equation $x^{2} + 5 x - 3 = 0$ ,
then the equation whose roots are $α γ + β δ$ and $α δ + β γ$ , is
A $x^{2} - 15 x - 158 = 0$
B $x^{2} + 15 x - 158 = 0$
C $x^{2} - 15 x + 158 = 0$
D $x^{2} + 15 x + 158 = 0$
In $△ A B C$ , which is not right angled, if p=sinA sinB sinC = and q=cosA. cosB. cosC. Then the equation having roots tanA,tanB and tanC is
A $q x^{3} - p x^{2} + (1 + q) x - p = 0$
B $q x^{3} + 2 p x^{2} + q x - p = 0$
C $q x^{3} - p x^{2} + (2 + q) x + p q = 0$
D $q x^{3} - p x^{2} + q x + p = 0$