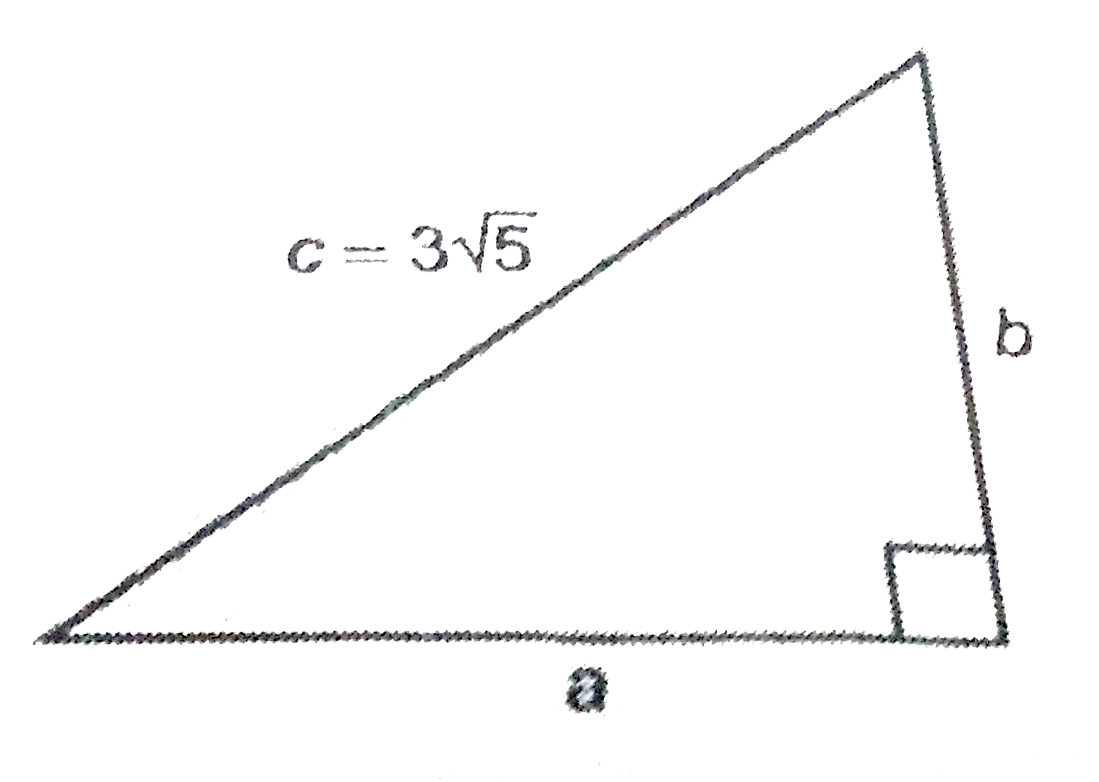
a, b and c are the integral sides of a right angled triangle in which c is the hypotenuse measuring $3 \sqrt{5}$ metres. If side 'a' is increased by $\frac{400}{3} %$ and side 'b' is increased by
$\frac{50}{3} %$ , then their total becomes 14 metres. Find the area of triangle.

Video Solution

Text Solution

Verified by Experts

By Pythagoras theorem,
$a^{2} + b^{2} = {(3 \sqrt{5})}^{2}$
$\Rightarrow a^{2} + b^{2} = 45 ... ... (1)$
Now length of base $= a + a \times \frac{400}{3} \times \frac{1}{100} = \frac{7 a}{3}$
and perpendicular $= b + b \times \frac{50}{3 \times 100} = \frac{7 a}{6}$
According to the problem, $\frac{7 a}{3} + \frac{7 a}{6} = 14$
$\Rightarrow 14 a + 7 b = 84 \Rightarrow b = 12 - 2 a$
Substituting this value in equation (1), we get
$a^{2} + {(12 - 2 a)}^{2} = 45$
$\Rightarrow a^{2} + 144 + 4 a^{2} - 48 a = 45$
$\Rightarrow 5 a^{2} - 48 a + 99 = 0$
$\Rightarrow 5 a^{2} - 15 a - 33 a + 99 = 0$
$\Rightarrow 5 a (a - 3) - 33 (a - 3) = 0$
$\Rightarrow (a - 3) (5 a - 33) = 0$
$∵ a = 3 or a = \frac{33}{5}$
But $a = \frac{33}{5}$ is not an integer.
So, we reject $a = \frac{33}{5}$
therefore a=3
Hence, $a = 3 m, b = 12 - 2 \times 3 = 6$
$∵ A r e a o f Δ = \frac{1}{2} a b = \frac{1}{2} \times 3 \times 6 = 9 m^{2}$

Updated on:21/07/2023