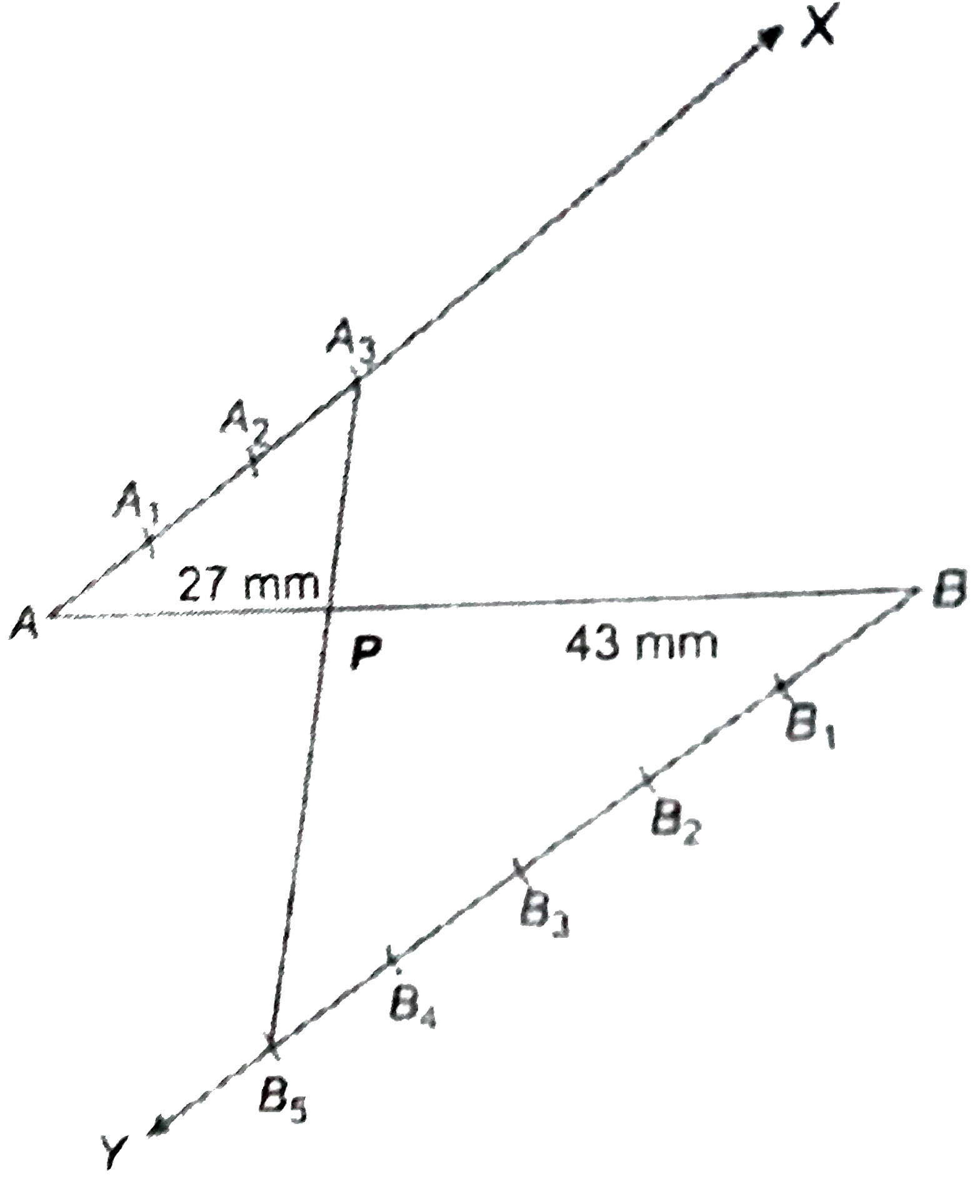
Draw a line segment of length 7 cm. Find a point P on it which divides it in the ratio $3 : 5 .$

Text Solution

Verified by Experts

Steps of Construction :
1. Draw a line segment Ab = 7 cm.
2. Draw $A X || B Y$ such that $∠ A and ∠ B$ are acute angles.
3. Divide AX and BY in 3 and 5 parts equally by compass and mark $A_{1}, A_{2}, A_{3}, B_{1}, B_{2}, B_{3}, B_{4} and B_{5}$ respectively.
4. Join $A_{3} B_{5}$ which intersect AB at P and divides $A P : P B = 3 : 5 .$
Hence P is the required point on AB which divide it in $3 : 5 .$
Verification (Justicicatio) : $I n Δ \forall_{3} P and Δ B B_{5} P$
$A X || B Y (by construction)$
$∠ A = ∠ B (alt.angles)$
$∠ A_{3} P A = ∠ B_{5} P B (vertically opp. angles)$
$∴ Δ A A_{3} P ~ Δ B B_{5} P (by AA criterion of similarity)$
$\Rightarrow \frac{A A_{3}}{B B_{5}} = \frac{A P}{B P} (let ecah equal part = c cm ∴ A A_{1} = A_{1} A_{2} = B_{1} B_{2} ... = x)$
$\Rightarrow \frac{3 x}{5 x} = \frac{A P}{B P} < b r > \Rightarrow A P : B P = 3 : 5$

|

Class 10 MATHS CONSTRUCTIONS

Topper's Solved these Questions

Similar Questions

NAGEEN PRAKASHAN-CONSTRUCTIONS-PROBLEMS FROM NCERT/ EXEMPLAR

Home
Ask Doubt
Profile