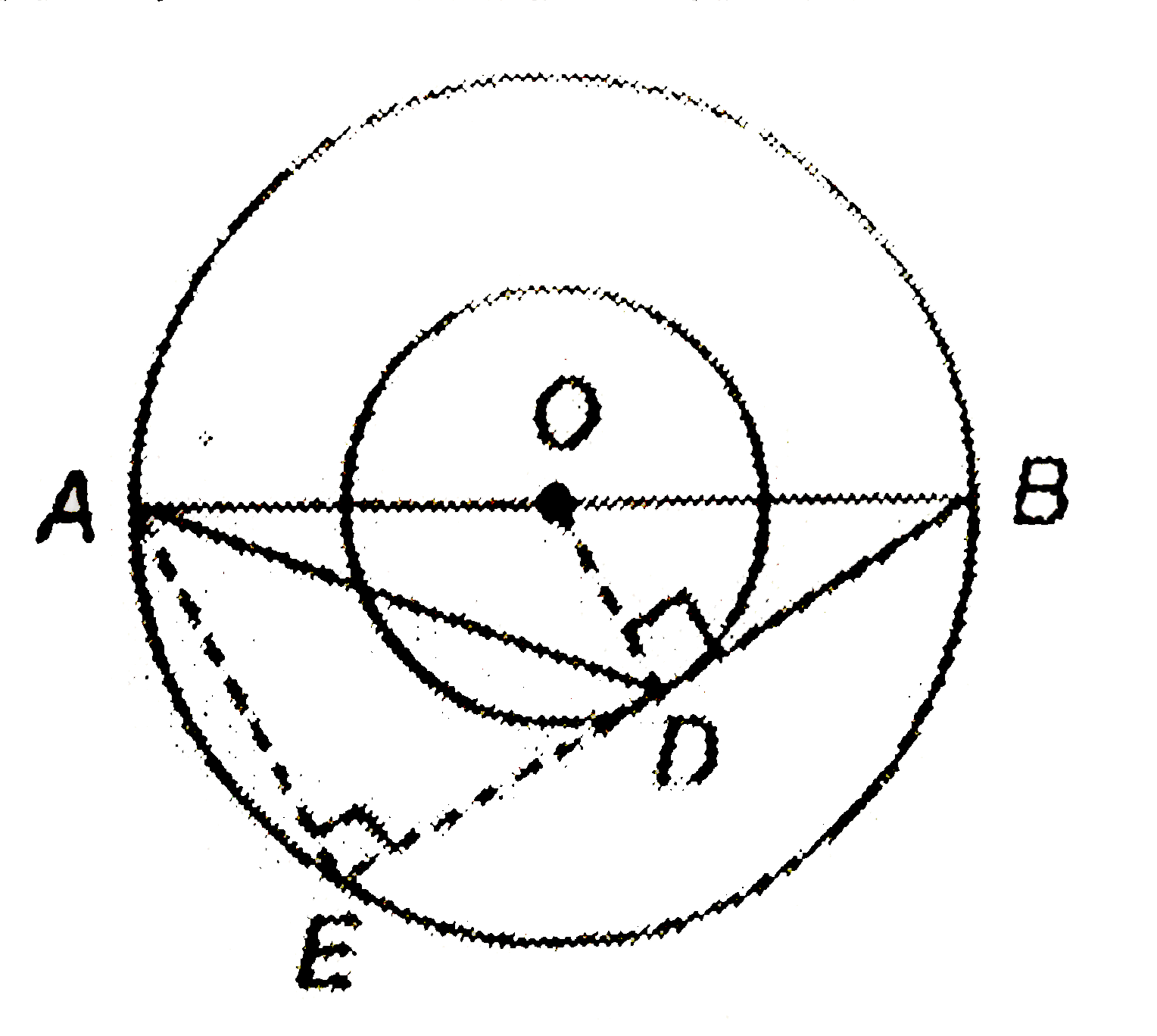
The radii of two concentric circles are 13cm and 8cm, AB is a diameter of bigger circle. BD is a tangent to the smaller circle touching it at D. Find the length AD.
Produce BD to E which cuts the circle at E. Join AE and OD. Since AB is the diameter of bigger circle.
∴ ∠AEB=90∘ (angle in a semicircle is right angle)
Also, ∠ODB=90∘ (radius through point of contact is ⊥ to the tangent)
Now, in △BOD and △BAE
∠B=ANGLEB (common)
∠ODB=∠AEB (EACH 90∘)
∴ △BOD~△BAE (AA corollary)
∴ ODAE=OBAB (corresponding sind of similar triangles are proportional)
⇒ 8AE=r2r ⇒ AE=16cm
Since, OD⊥EB
∴ DE=DB (⊥ drawn from the centre to the chord bisects the chord)
In right △ODB,
DB2=OB2−OD2
=(13)2−(8)2=169−64=105
∴ DB=√105cm=ED
Now, in right △AED, by Pythagoras theorem
AD2=AE2+ED2
⇒ AD2=(16)2+105=256+105=361
⇒ AD=√361 i.e., 19cm
Hence, AD=19cm.
Topper's Solved these Questions
- CIRCLESBOOK - NAGEEN PRAKASHANCHAPTER - CIRCLESEXERCISE - Problems From NCERT/exemplar
11 Videos
- CIRCLESBOOK - NAGEEN PRAKASHANCHAPTER - CIRCLESEXERCISE - Exercise
25 Videos
- ARITHMETIC PROGRESSIONBOOK - NAGEEN PRAKASHANCHAPTER - ARITHMETIC PROGRESSIONEXERCISE - Revision Exercise Long Answer Question
5 Videos
- CO-ORDINATE GEOMETRYBOOK - NAGEEN PRAKASHANCHAPTER - CO-ORDINATE GEOMETRYEXERCISE - Revision Exercise Short Answer Questions
9 Videos
Similar Questions
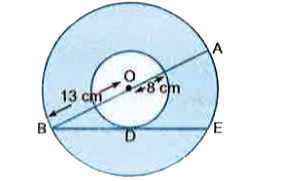
The radii of two concentric circles are 13 cm and 8 cm. AB is a diameter of the bigger circle. BD is a tangent to the smallest circle touching it at D. Find the length AD.
View SolutionIn Fig., the radii of two concentric circles are 13 cm and 8 cm. AB is diameter of the bigger circle. BD is the tangent to the smaller circle touching it at D. Find the length of AD.
View Solution
Knowledge Check
The radii of two concentric circle are 13 cm and 8 cm. AB is a diameter of the bigger circle and BD is a tangent to the smaller circle touching it at D and the bigger circle at E. Point A is joined to D. Find the length of AD.
A20 cmB19 cmC18 cmD17 cmThe radii of two concentric circle are 13 cm and 8 cm. AB is a diameter of the bigger circle and BD is a tangent to the smaller circle touching it at D and the bigger circle at E. Point A is joined to D. Find the length of AD.
A20 cmB19 cmC18 cmD17 cmThe radius of two concentric circles are 9 cm and 15 cm. If the chord of the greater circle be a tangent to the smaller circle, then the length of that chord is
A24 cmB12 cmC30 cmD18 cm
The radii of two concentric circle are 13 cm and 8 cm. AB is a diameter of the bigger circle and BD is a tangent to the smaller circle touching it at D and the bigger circle at E. Point A is joined to D. Find the length of AD.
View SolutionThe radii of two co-centric circles are 13 cm and 8 cm respectively. AB is diameter of outer circle and BE is tangent to the inner circles which touches the inner circle at point D. Then find the length of AD.
View SolutionIf radii of two concentric circles are 12 cm and 13 cm, find the length of each chord of one circle which is tangent to the other circle.
View SolutionIf the radii of two concentric circles are 4 cm and 5 cm, then find the length of each chord of one circle which is tangent to the other circle.
View SolutionIf radii of two concentric circles are 4 cm and 5 cm Then the length of the chord of one circle which is tangent to the other circle is
View Solution
