Find a point on the line through A(5,−4)andB(−3,2), that is, twice as far from A as from B.
Let P(x,y) be a point on AB such that
PA=2PB

⇒ PAPB=21 ⇒ PA:PB=2:1
So, by using section formula for internal division,
x=mx2+nx1m+n,y=my2+ny1m+n
⇒ x=2(−3)+1(5)2+1⇒ x=−13
and y=2(2)+1(−4)2+1⇒ y=0
⇒ Required point ≡(−13,0)
BUT
This is not the end of this question.
Think : Is it not possible that P(x,y) divides AB externally in the ratio 2 : 1.

So, by using section formula for external division,
∴ x=2(−3)−1(5)2−1⇒ x=−111⇒ x=−11
and y=2(2)−1(−4)2−1⇒ y=81⇒ y=8
So, co-ordinates of p are (-11, 8) also.
Hence, required points are (−13,0)and(−11,8).
Topper's Solved these Questions
- CO-ORDINATE GEOMETRYBOOK - NAGEEN PRAKASHANCHAPTER - CO-ORDINATE GEOMETRYEXERCISE - Miscellaneous Examples
8 Videos
- CO-ORDINATE GEOMETRYBOOK - NAGEEN PRAKASHANCHAPTER - CO-ORDINATE GEOMETRYEXERCISE - Problems Of NCERT/exemplar
14 Videos
- CIRCLESBOOK - NAGEEN PRAKASHANCHAPTER - CIRCLESEXERCISE - Revision Exercise Long Answer Questions
3 Videos
- CONSTRUCTIONSBOOK - NAGEEN PRAKASHANCHAPTER - CONSTRUCTIONSEXERCISE - PROBLEMS FROM NCERT/ EXEMPLAR
10 Videos
Similar Questions
Knowledge Check
Find the coordinates of a point lying between the points P(3, -4) and Q(-2, 5) that is twice as far from P as from Q.
A(-7, 14)B(7, -14)C(-1/3, 2)D(1/3, -2)
Find the coordinates of points lying on the line joining P(3,−4) and Q(−2,5) that is twice as far from P as Q
View SolutionFind the coordinates of points lying on the line joining P(3,−4) and Q(−2,5) that is twice as far from P as Q
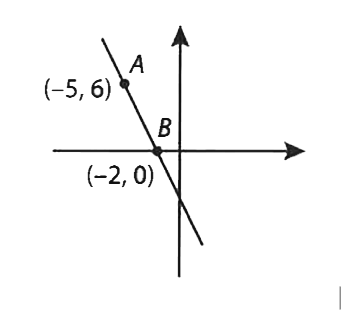
View SolutionWhat are the coordinates for the point on the line AB (see figure) that is three times as far from A as from B, and that is in between point A and B?
View SolutionFind the two points on the line through the points A(1,2,3)andB(3,5,9) at a distance of 14 units from the mid point of AB.
View SolutionFind the points on the line through the points A (1,2,3) and B ( 5,8 ,15) at a distance of 14 units from the mid-point of AB.
View SolutionThe coordinatse of two points A and B are (−1,4)and(5,1), respectively. Find the coordinates of the point P which lie on extended line AB such that it is three times as far from B as from A.
View SolutionThe coordinatse of two points A and B are (−1,4)and(5,1), respectively. Find the coordinates of the point P which lie on extended line AB such that it is three times as far from B as from A.
View Solution
