Find the median of the following frequency distibution :
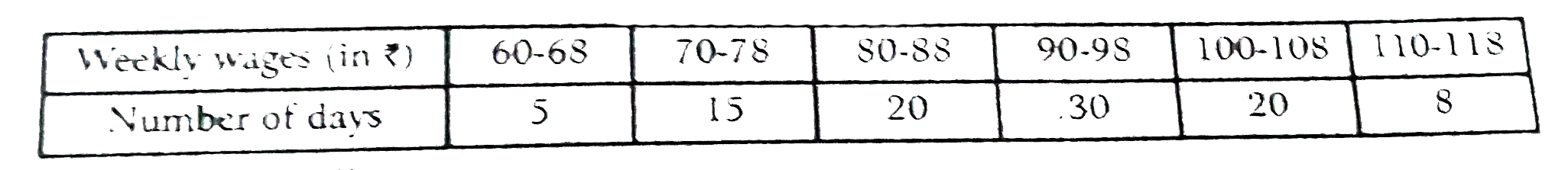
Text Solution
First of all we will prepare an exclusive series from the given (inclusive) series. To make it we subtract and add the same number, i.e.,70−682=1 in each class. So, new table is :

Here, N2=982=49
So, cumulative frequency just greater than or equal to 49 is 70 and its corresponding class is the medianl class.
∴ Median=l1+N2−Cf×i=89+49−4030×10+3=92
|
Topper's Solved these Questions
- STATISTICS BOOK - NAGEEN PRAKASHANCHAPTER - STATISTICS EXERCISE - Problems From NCERT/exemplar
4 Videos
- STATISTICS BOOK - NAGEEN PRAKASHANCHAPTER - STATISTICS EXERCISE - Exercise 14 A
17 Videos
- SOME APPLICATIONS OF TRIGONOMETRYBOOK - NAGEEN PRAKASHANCHAPTER - SOME APPLICATIONS OF TRIGONOMETRYEXERCISE - Long Answer Questions
5 Videos
- TRIANGLES BOOK - NAGEEN PRAKASHANCHAPTER - TRIANGLES EXERCISE - Revision Exercise Long Questions
4 Videos
Similar Questions
Find the median for the following frequency distribution

View SolutionFind the median for the following frequency distribution:
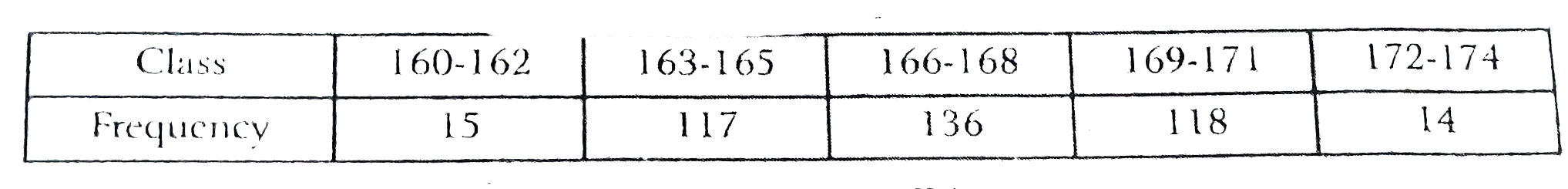
View SolutionFind the median for the following frequency distribution:

View SolutionFind the median for the following frequency distribution:
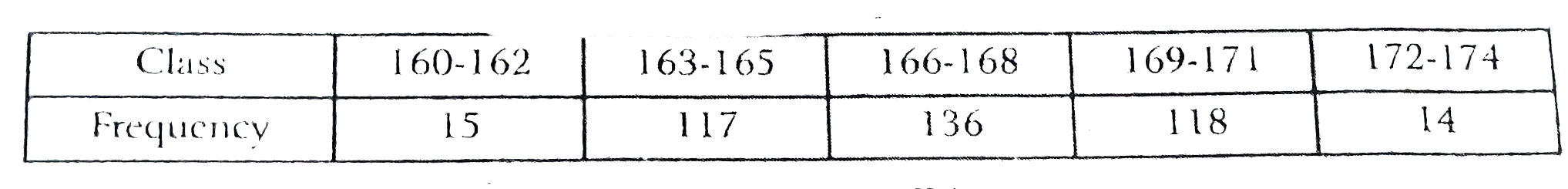
View SolutionFind the median for the following frequency distribution

View SolutionFind the median for the following frequency distribution:
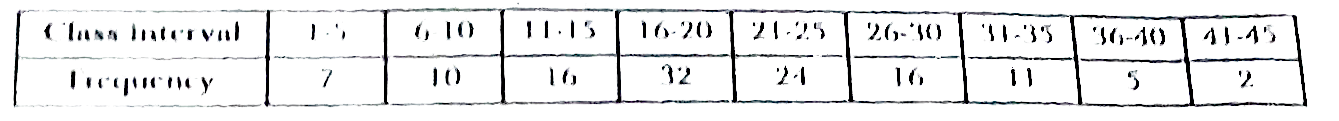
View SolutionFor the following frequency distibution .

View SolutionFind the median of the following frequency table :
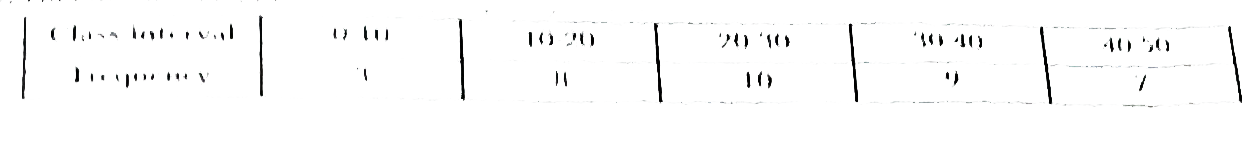
View SolutionFind the median of the following frequency table :

View SolutionFind the median of the following frequency table :

View Solution
