The angle of elevation of the top of a tower 30 m high from the foot of another tower in the same plane is 60∘ and the angle of elevation of the top of the second tower from the foot of the first tower is 30∘. Find the distance between the two towers and also the height of the other tower.
Let AB and CD be two tower.
Given that
CD=30m,∠CBD=60∘ and ∠ACB=30∘
In ΔABC,
tan60∘=CDBC⇒√3=30BC
⇒BC=30√3=10√3m
∴ The distance between two towers =10√3m
In ΔABC
tan30∘=ABBC⇒1√3=AB10√3⇒AB=10m
∴ Height of other tower =10m
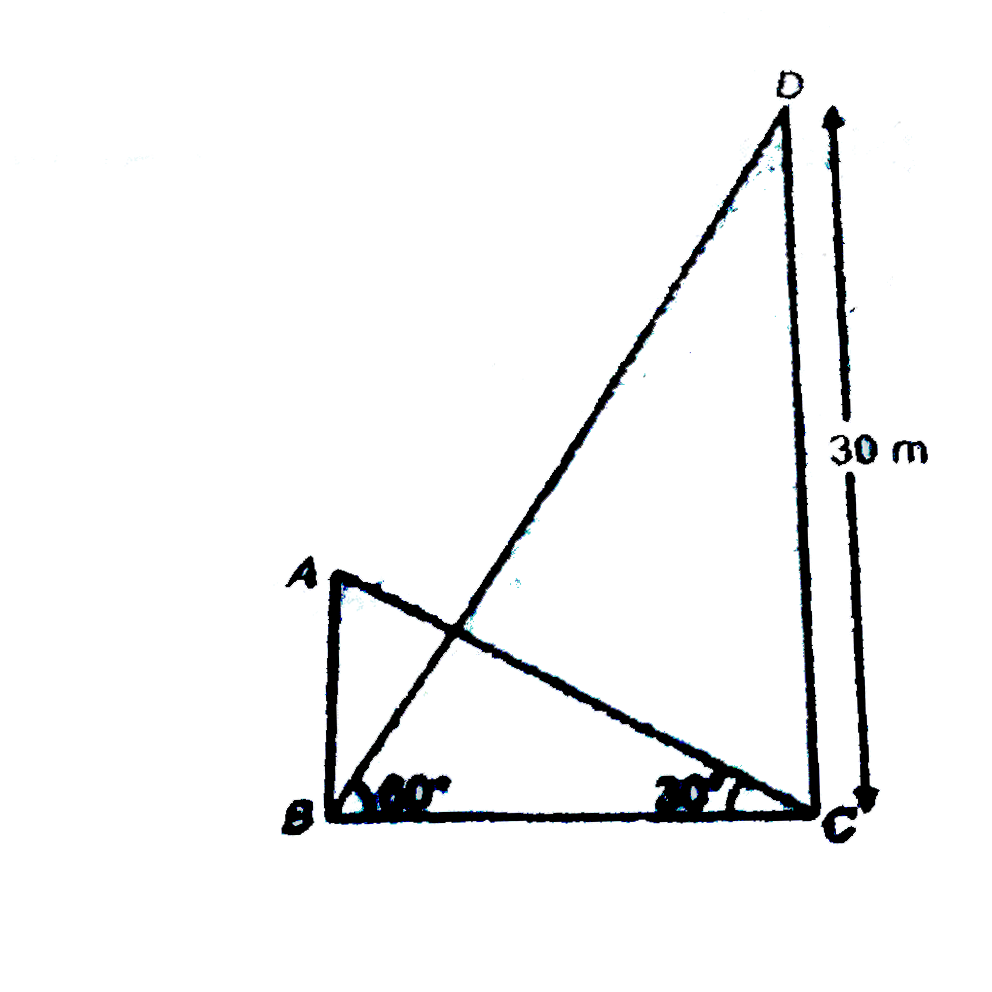
Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHANCHAPTER - SOME APPLICATIONS OF TRIGONOMETRYEXERCISE - Exercise32videos
SOME APPLICATIONS OF TRIGONOMETRY
- BOOK - NAGEEN PRAKASHANCHAPTER - SOME APPLICATIONS OF TRIGONOMETRYEXERCISE - Revision Exercise (short Answer Questions)5videos
SOME APPLICATIONS OF TRIGONOMETRY
- BOOK - NAGEEN PRAKASHANCHAPTER - REAL NUMBERSEXERCISE - Revision Exercise Long Answer Questions5videos
REAL NUMBERS
- BOOK - NAGEEN PRAKASHANCHAPTER - STATISTICS EXERCISE - Revision Exercise Long Answer Questions5videos
STATISTICS
Similar Questions
The angle of elevation of the top of a tower 30 m high from the foot of another tower in the same plane is 60∘ and the angle of elevation of the top of the second tower from the foot of the first tower is 30∘. Find the distance between the two and also the height of the tower.
View SolutionThe angle of elevation of the top of a tower 30 m high from the foot of another tower in the same plane is 60∘ and the angle of elevation of the top of the second tower from the foot of the first tower is 30∘. The distance between the two towers is m times the height of the shorter tower. What is m equal to ?
View Solution
Knowledge Check
- Question 1 - Select One
The angle of elevation of the top of a tower 30 m high from the foot of another tower in the same plane is 60∘ and the angle of elevation of the top iof the second tower from the foot of the first tower is 30∘. The distance between the two towers isntimes the height of the shorter tower. What is nequal to?
A√2B√3C12D13 - Question 2 - Select One
The angle of elevation of the top of a tower of height H from the foot of another tower in the same plane is 60∘ and the angle of elevation of the top of the second tower from the foot of the first tower is 30∘. If h is the height of the other tower, then which one of the following is correct?
AH=2hBH=√3hCH=3hDNone of the above - Question 3 - Select One
The angle of elevation of the top of a tower of height H from the foot of another tower in the same plane is 60∘ and the angle of elevation of the top of the second tower from the foot of the first tower is 30∘. If is the height of the other tower is h , then which one of the following is correct?
AA. H=2hBB. H=√3hCC. H=3hDD. None of these
The angle of elevation of the top of a building from the foot of the tower is 30∘ and the angle of elevation of the top of the tower from the foot of the building is 45∘. If the tower is 30 m high, find the height of the building.
View SolutionThe angle of elevation of the top of a building from the foot of the tower is 30∘and the angle of elevation of the top of the tower from the foot of the building is 60∘. If the tower is 50 m high, find the height of the building.
View SolutionThe angle of elevation of the top of a building from the foot of tower is 30∘ and the angle of elevation of the top of the tower from the foot of the building is 60∘. It the tower is 30 m high, then the height of the building is
View SolutionThe angle of elevation of the top of a building from the foot of the tower is 30∘ and the angle of elevation of the top of tower from the foot of the building is 60∘,If the tower is 50 m high, find the height of the building.
View SolutionThe angle of elevation of the top of a hill from the foot of a tower is 60∘ and the angle of elevation of the top of the tower from the foot of the hill is 30∘. If the tower is 50 m high, then what is the height of the hill?
View Solution

