Prove that the circle drawn on any one of the equal sides of an isosceles triangle as diameter bisects the base.

Video Solution

Text Solution

Verified by Experts

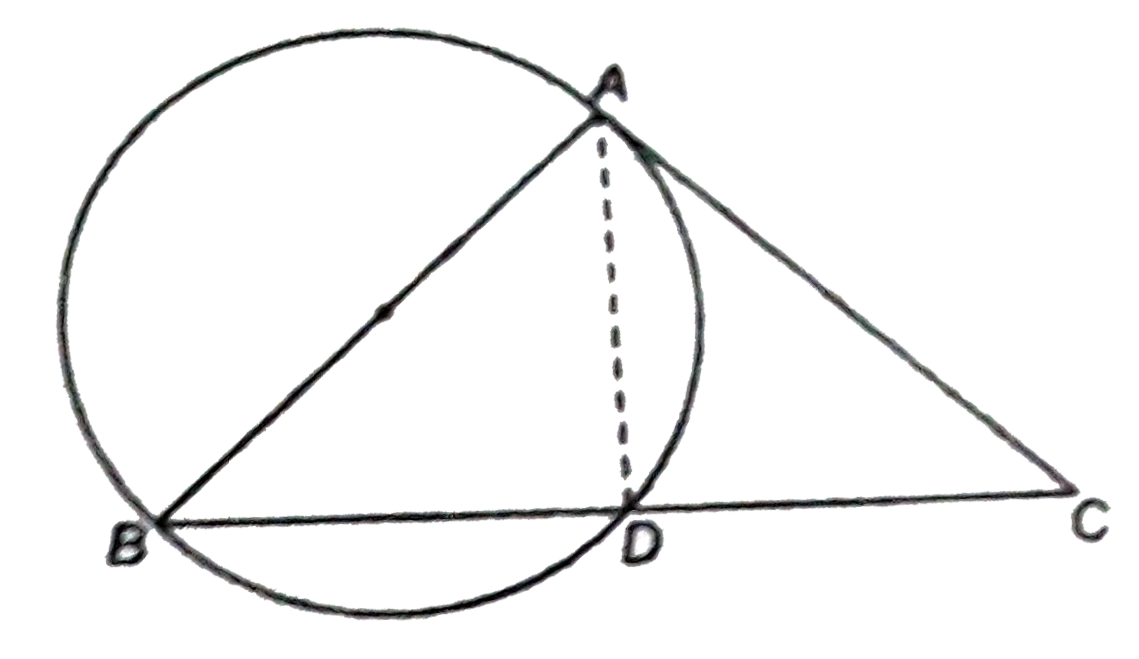
Given : $A$ $Δ A B C$ in which $A B = A C$ and a circle is drawn by taking AB as diameter which intersects the side BC of triangle at D.
To prove : $B D = D C$
Construction: Join AD.
Proof: Since angle in a semi-circle is a right angle, therefore
$∠ A D B = 90^{\circ}$
Now, in $Δ A B D$ and $Δ A C D$ , we have
$A B = A C$ (given)
$∠ A D B = A D$ (each equal to $90^{\circ}$ )
and, $A D = A D$ (Common)
$\Rightarrow Δ A B D ≅ Δ A C D$ (by $S A S$ congruency)
$\Rightarrow B D = D C$

Updated on:21/07/2023