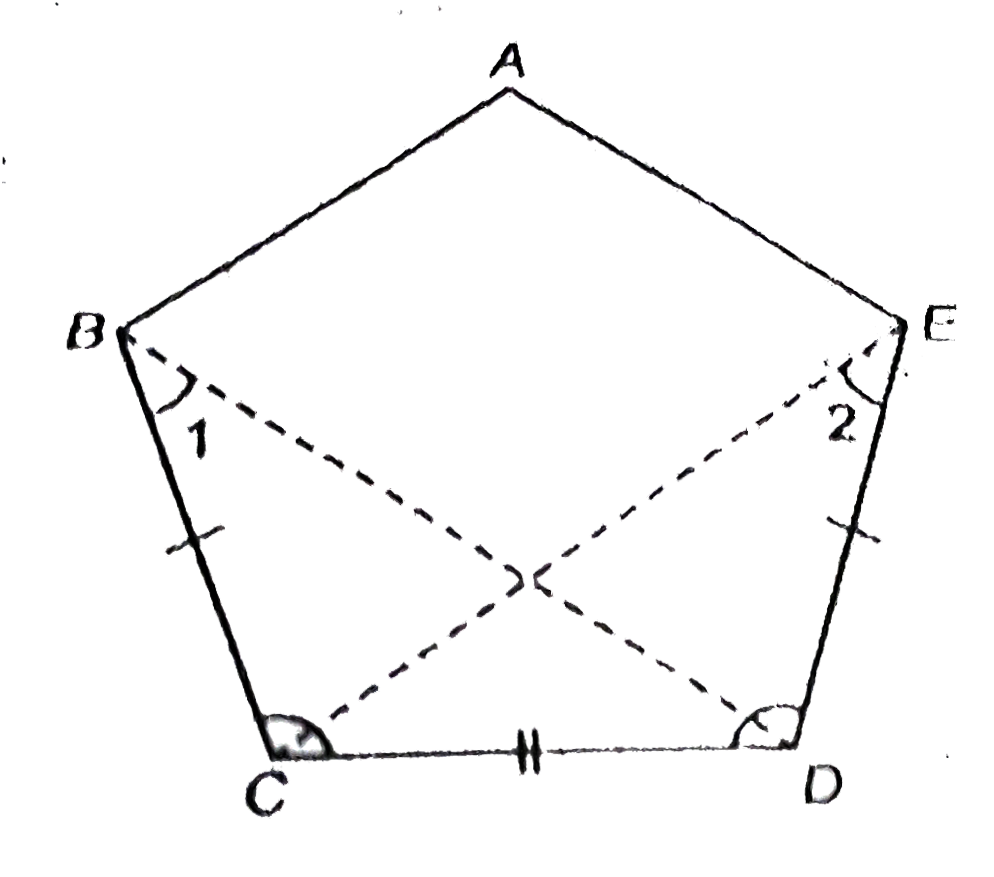
Prove that any four vertices of a regular pentagon are concyclic.
Given: a regular pentagon ABCDE.
To prove: Any four vertices of the pentagon ABCDE are concyclic.
Construcation: Join BD and CE.
Proof : In ΔBCD and ΔECD, we have
BC=ED (sides of a regular pentagon)
∠C=∠D (angles of regular pentagon)
CD=CD (common sides)
ΔBCD≅ΔCDE (by SAS criterion of congruence)
∴∠1−∠2
But they are subtended by CD on the same of it.
∴ Points B,C,D,E are concyclic.
Similarly, it can be proved that any other four vertices of the pentagon ABCDE are concyclic.
Topper's Solved these Questions
- CIRCLE BOOK - NAGEEN PRAKASHANCHAPTER - CIRCLE EXERCISE - Exercise 10a
22 Videos
- CIRCLE BOOK - NAGEEN PRAKASHANCHAPTER - CIRCLE EXERCISE - Exercise 10b
19 Videos
- AREA OF PARALLELOGRAMS AND TRIANGLESBOOK - NAGEEN PRAKASHANCHAPTER - AREA OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Revision Exercise (long Answer Question)
5 Videos
- CO-ORDINATE GEOMETRY BOOK - NAGEEN PRAKASHANCHAPTER - CO-ORDINATE GEOMETRY EXERCISE - Exercise
8 Videos
Similar Questions
Knowledge Check
The least angle of rotation of a regular pentagon
A72∘B90∘C180∘D360∘Order of rotation of a regular pentagon is
A1B5C4D0Find each interior of a regular pentagon.
A108∘B105∘C103∘D101∘
Four particles each having a charge q are placed on the four vertices of a regular pentagon. The distance of each comer from !be centre is 'a'. Find the electric field at the centre of pentagon.
View SolutionFive point masses m each are kept at five vertices of a regular pentagon. Distance of centre of pentagon from any one of the verticle is 'a'. Find gravitational potential and filed strength at centre.
View SolutionProve that the interior angle of a regular pentagon is three times exterior anles of a regular decagon.
View SolutionFive identical charges, q1 each, are placed at the vertices of a regular pentagon having side length l1. The net electrostatic force on any of the charges due to other four is F1. Find the electrostatic force F2 on any one of the five identical charges, q2 each, placed at the vertices of a regular pentagon having side length l2.
View SolutionAssertion : Five charges +q each are placed at five vertices of a regular pentagon. A sixth xharge −Q is placed at the centre of pentagon. Then, net electrostatic force on −Q is zero.
Reason : Net electrostatic potential at the centre is zero.
View Solution
