In the adjoining figure, D,E and F are the mid- points of the sides of ΔPQR and S is the foot of perpendicular form P to side S.
Prove that:
(i) FQ=FS and ∠FQS=∠FSQ.
(ii)∠FQS=∠FED.
(iii) square FSDE is a cyclic quadrilateral.
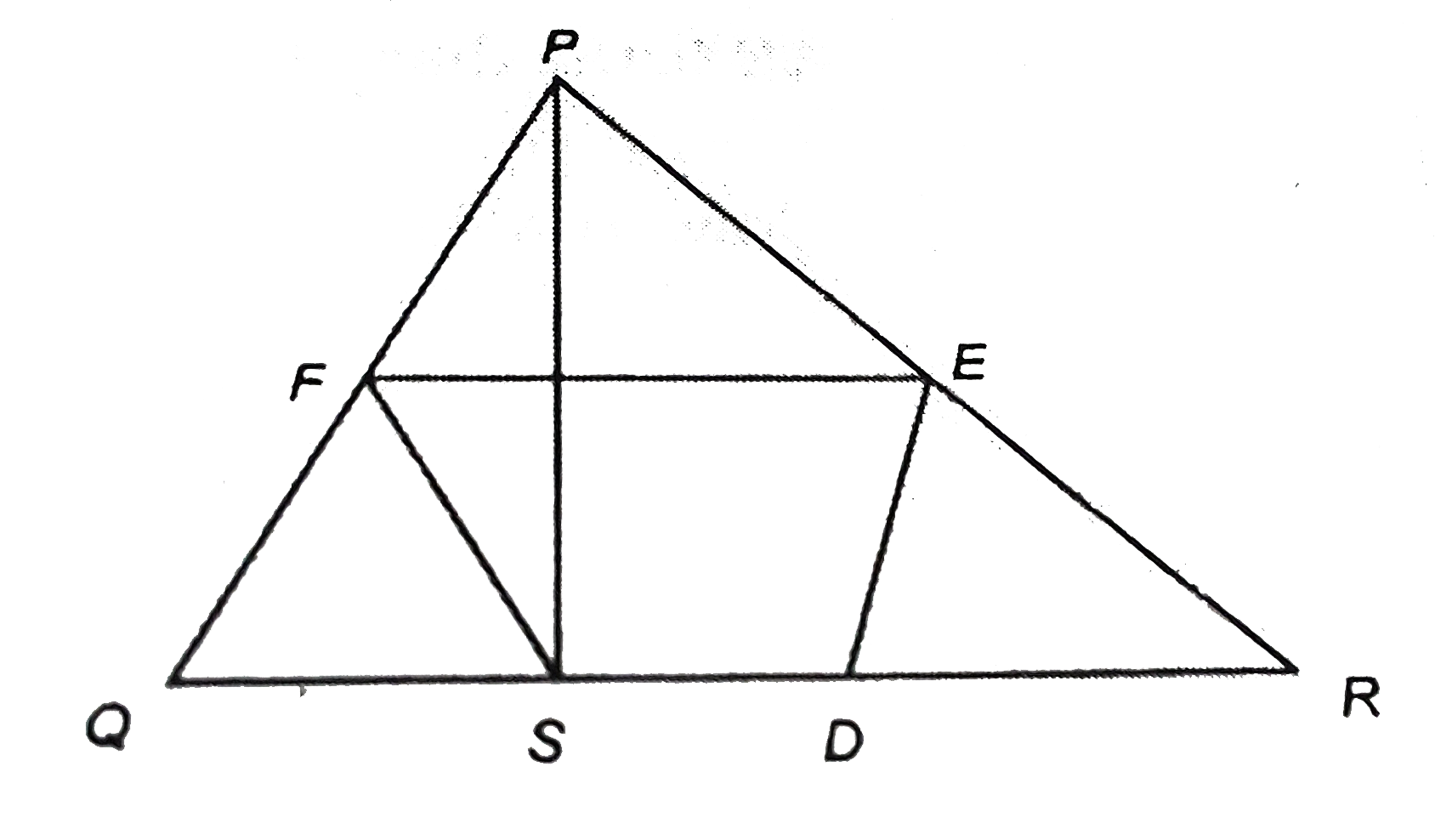
(i) PS⊥QR
⇒∠PSQ=90∘
F is the mid-point of PQ.
∴FS=12PQ or FS=FP
Now, ΔPQS is right-angled triangle and we know that the mid-point of hypotenuse is equidistant form the vertices of a triangle.
∴FQ=FP=FS
⇒FQ=FS
⇒∠FSQ=∠FQS ..........(1)
(ii) F is the mid-point of PQ and E is the mid-point of PR.
∴FE| |QR
⇒FE| |QD
Similarly, FQ| |ED
∴□FEDQ is a parallelogram.
We know that opposite angles of a parallelogram are equal.
∴∠FQS=∠FED
(iii) Now from eqs. (1) and (2),
∠FSQ=∠FED
But ∠FSQ is the exterior angle of square FSDE.
square FSDE is a cyclic quadrilateral.
Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHANCHAPTER - CIRCLE EXERCISE - Exercise 10a22videos
CIRCLE
- BOOK - NAGEEN PRAKASHANCHAPTER - CIRCLE EXERCISE - Exercise 10b19videos
CIRCLE
- BOOK - NAGEEN PRAKASHANCHAPTER - AREA OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Revision Exercise (long Answer Question)5videos
AREA OF PARALLELOGRAMS AND TRIANGLES
- BOOK - NAGEEN PRAKASHANCHAPTER - CO-ORDINATE GEOMETRY EXERCISE - Exercise8videos
CO-ORDINATE GEOMETRY
Similar Questions
In the adjoining figure, D,E and F are the mid- points of the sides of ΔPQR and S is the foot of perpendicular form P to side S.
Prove that:
(i) FQ=FS and ∠FQS=∠FSQ.
(ii)∠FQS=∠FED.
(iii) square FSDE is a cyclic quadrilateral.
 View Solution
View SolutionIn the adjoining figure D, E and F are the mid - points of the sides BC, AC and AB respectively to triangle. Show that ∠EDF=∠A, ∠DEF=∠B and ∠DFE=∠C:
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
If D,E and F are the mid-points of the sides BC,CA and AB, respectively of a ΔABC and O is any point, show that
(i) AD+BE+CF=0
(ii) OE+OF+DO=OAAA. a zero vectorBB. a unit vectorCC. 0DD. none of these
In the adjoining figure D, E and F are the mid-points of the sides BC, AC and AB respectively. △DEF is congruent to triangle :
 View Solution
View SolutionIn the figure, D E and F are midpoints of sedes AB,BC and AC respectively. P is the foot of the perpendicular from A to side BC. Show that points D, E,F and P are concyclic.
 View Solution
View SolutionIn the adjoining figure D, E and F are the mid-points of the sides BC, CA and AB of the equilateral ΔABC. Prove that ΔDEF is also an equilateral triangle.
 View Solution
View SolutionIn the adjoining figure D, E and F are the mid-points of the sides BC, CA and AB respectively of ΔABC. Prove that:
(i) □BDEF is a parallelogram
(ii) area of ΔDEF=14× area of ΔABC
(iii) area of □BDEF=12× area of ΔABC
 View Solution
View SolutionIn the adjoining figure, D is the mid-point of side AB of ΔABC and P be any point on side BC. If CQ∣∣PD, then prove that:
area of ΔBPQ=12× area of ΔABC
 View Solution
View SolutionIn the given figure, S and T are points on sides PR and QR of ΔPQR such that ∠P=∠RTS. Show that ΔRPQ~ΔRTS.
 View Solution
View SolutionIn the given figure, points S,T and U are the midpoints of sides PQ,QR and PR respectively. IF PV⊥QR, then prove that □ SVTU is a cyclic quadrilateral.
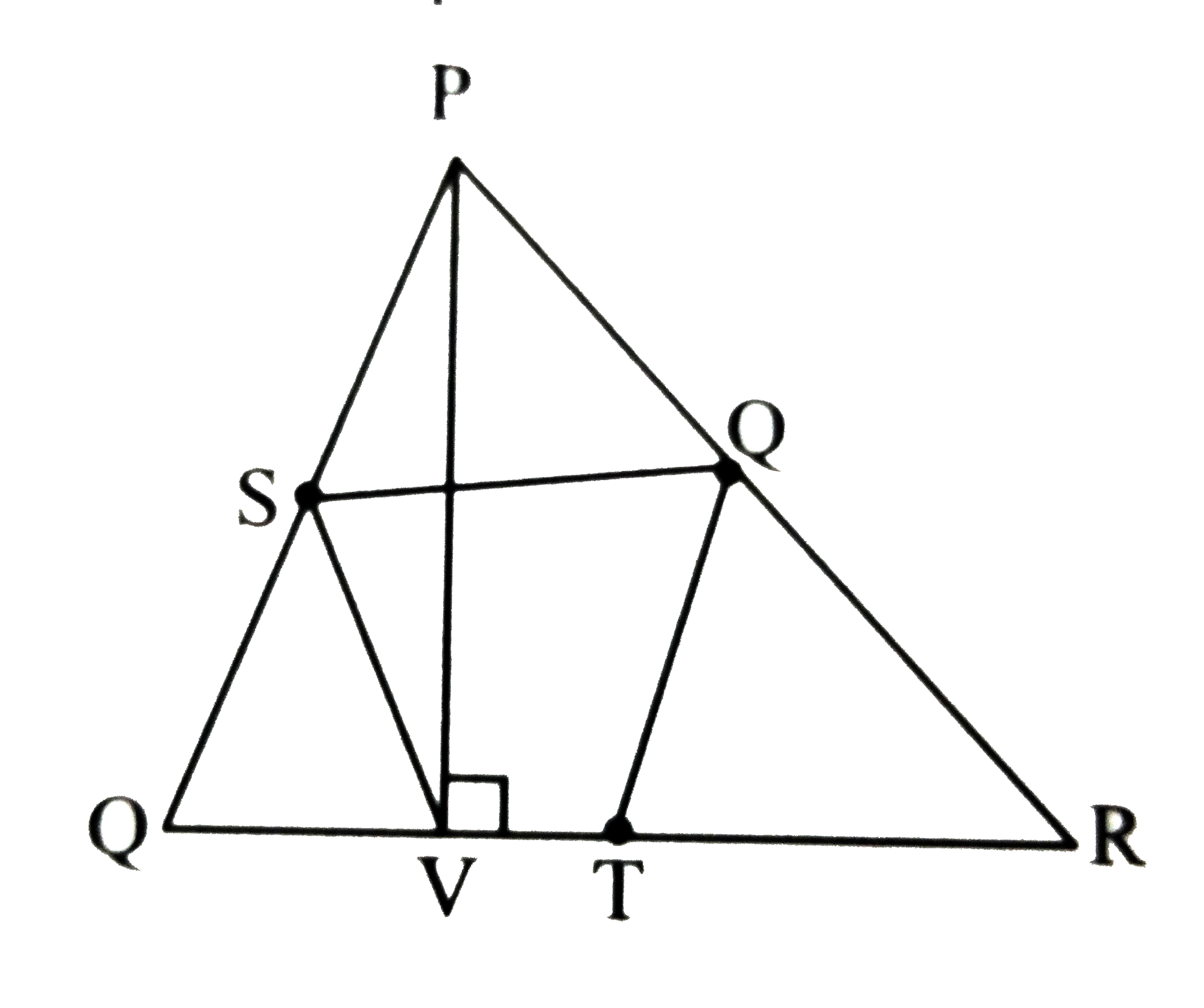 View Solution
View Solution

