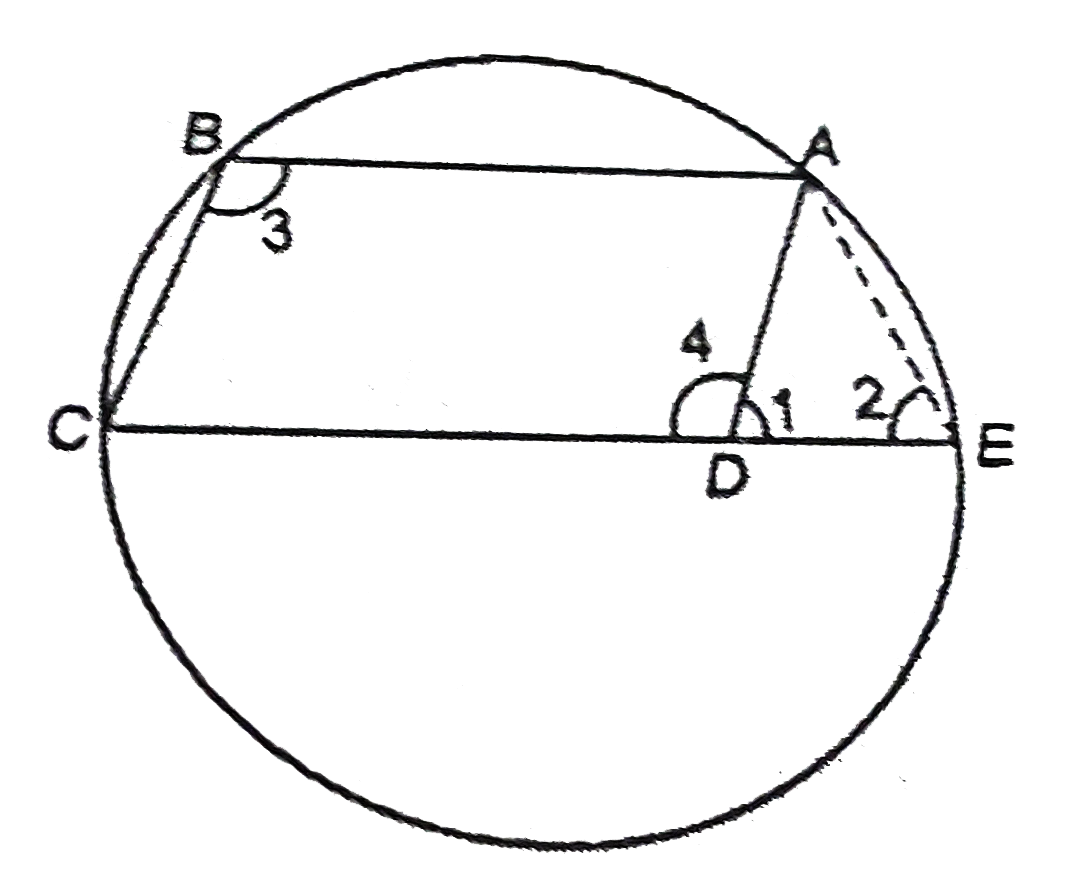
ABCD is a parallelogram . The circle passing through the vertices. A, B and C intersects CD (or CD produced) at E. Prove that AE=AD.
∠1+∠4=180∘ (L.P.A.) ......(1)
∠2+∠3=180∘ ........(2)
(sum of opposite of a cyclic quadrilateral is 180∘)
∴ From (1) and (2), we get
∠1+∠4=∠2+anl≥3 ......(3)
But (opposite angles of a parallelogram )
∴ From (3) and (4) ,
∠1+∠4=∠2+∠4
⇒∠1=∠2
⇒AE=AD (∵ sides opposite to equal angles are equal)
Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHANCHAPTER - CIRCLE EXERCISE - Exercise 10a22videos
CIRCLE
- BOOK - NAGEEN PRAKASHANCHAPTER - CIRCLE EXERCISE - Exercise 10b19videos
CIRCLE
- BOOK - NAGEEN PRAKASHANCHAPTER - AREA OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Revision Exercise (long Answer Question)5videos
AREA OF PARALLELOGRAMS AND TRIANGLES
- BOOK - NAGEEN PRAKASHANCHAPTER - CO-ORDINATE GEOMETRY EXERCISE - Exercise8videos
CO-ORDINATE GEOMETRY
Similar Questions
ABCD is a parallelogram. The circle through A,BandC intersects CD produced at E, prove that AE=AD.
View SolutionABCD is a parallelogram. The circle through A, B and C intersect CD (produced ifnecessary) at E. Prove that AE = AD.
View SolutionABCD is a parallelogram. The circle through A,B and intersects CD produced at E. show that AD =AE.
View SolutionABCD is a parallelogram. A circle through A, B is so drawn that it intersects AD at P and BC at Q. Prove that P, Q, C and D are concyclic.
View SolutionP is the mid-point of the side CD of a parallelogram ABCD. A line through C parallel to PA intersects AB at Q and DA produced at R. Prove that DA = AR and CQ = QR.
View SolutionABCD is a quadrilateral. The straight line through C parallel to the diagonal DB intersects AB produced at E. Prove that the ar(quad. ABCD) = ar(△ADE).
 View Solution
View SolutionIn Figure, ABCD is a cyclic quadrilateral. A circle passing through A and B meets AD and BC in the points E and F respectively. Prove that EFDC
View SolutionThrough the mid-point M of the side CD of a parallelogram ABCD , the line BM is drawn intersecting AC at LandAD produced at E . Prove that EL=2BL.
View SolutionCommon tangents AB and CD to two circles intersects at E. Prove that AB=CD
View SolutionIn a circle with centre O, chords ABandCD intersect inside the circumference at E. Prove that ∠AOC+∠BOD=2∠AEC.
View Solution

