Prove that the chords inclined on the same angle to the radius or diameter of a circle are equal in length.
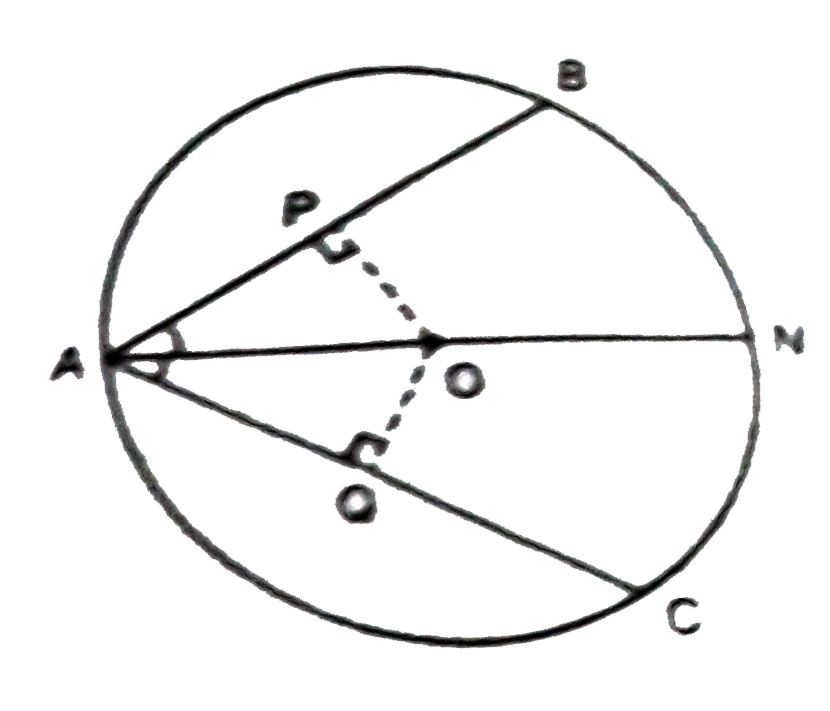
Given: AB and AC are two chords of a circle with centre O, AN is the diameter of the circle and ∠BAN=∠CAN
To Prove: AB=AC
Construction : Draw OP⊥AB and OQ⊥AC.
Proof: In ΔOPA and ΔOQA,
∵ ⎧⎪⎨⎪⎩∠OPA=∠OQA(each 90∘)∠OAP=∠OAQ(given)OA=OA(common)
∴ΔOPA≅ΔOQA(A.A.S.congruency)
⇒OP=OQ (c.p.c.t)
Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHANCHAPTER - CIRCLE EXERCISE - Exercise 10a22videos
CIRCLE
- BOOK - NAGEEN PRAKASHANCHAPTER - CIRCLE EXERCISE - Exercise 10b19videos
CIRCLE
- BOOK - NAGEEN PRAKASHANCHAPTER - AREA OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Revision Exercise (long Answer Question)5videos
AREA OF PARALLELOGRAMS AND TRIANGLES
- BOOK - NAGEEN PRAKASHANCHAPTER - CO-ORDINATE GEOMETRY EXERCISE - Exercise8videos
CO-ORDINATE GEOMETRY
Similar Questions
Knowledge Check
- Question 1 - Select One
Calculate the angle subtended by the chord at the point on the major arc if the radius and the chord of the circle are equal in length
AA) 30∘BB) 120∘CC) 200∘DD) 300∘ - Question 2 - Select One
A circle has two parallel chords of lengths 6 cm and 8 cm. If the chords are 1 cm apart and the centre is on the same side of the chords, then a diameter of the circles is of length:
A5 cmB6 cmC8 cmD10 cm - Question 3 - Select One
A circle has two parallel chords of lengths 6 cm and 8 cm. If the chords are 1 cm apart and the centre is on the same side of the chords, then a diameter of the circles is of length:
A5 cmB6 cmC8 cmD10 cm
prove that the line joining the mid-point of two equal chords of a circle subtends equal angles with the chord.
View SolutionProve that the tangents drawn at the end points of a chord of a circle make equal angles with the chord.
View SolutionIn two concentric circles prove that all chords of the outer circle which touch the inner circle are of equal length.
View SolutionIf a chord of a circle subtends an angle of 30∘ at the circumference of the circle, then what is the ratio of the radius of the circle and the length of the chord respectively?
View SolutionIf a chord of a circle subtends an angle of 30∘ at the circumference of the circle, then what is the ratio of the radius of the circle and the length of the chord respectively?
View Solution

