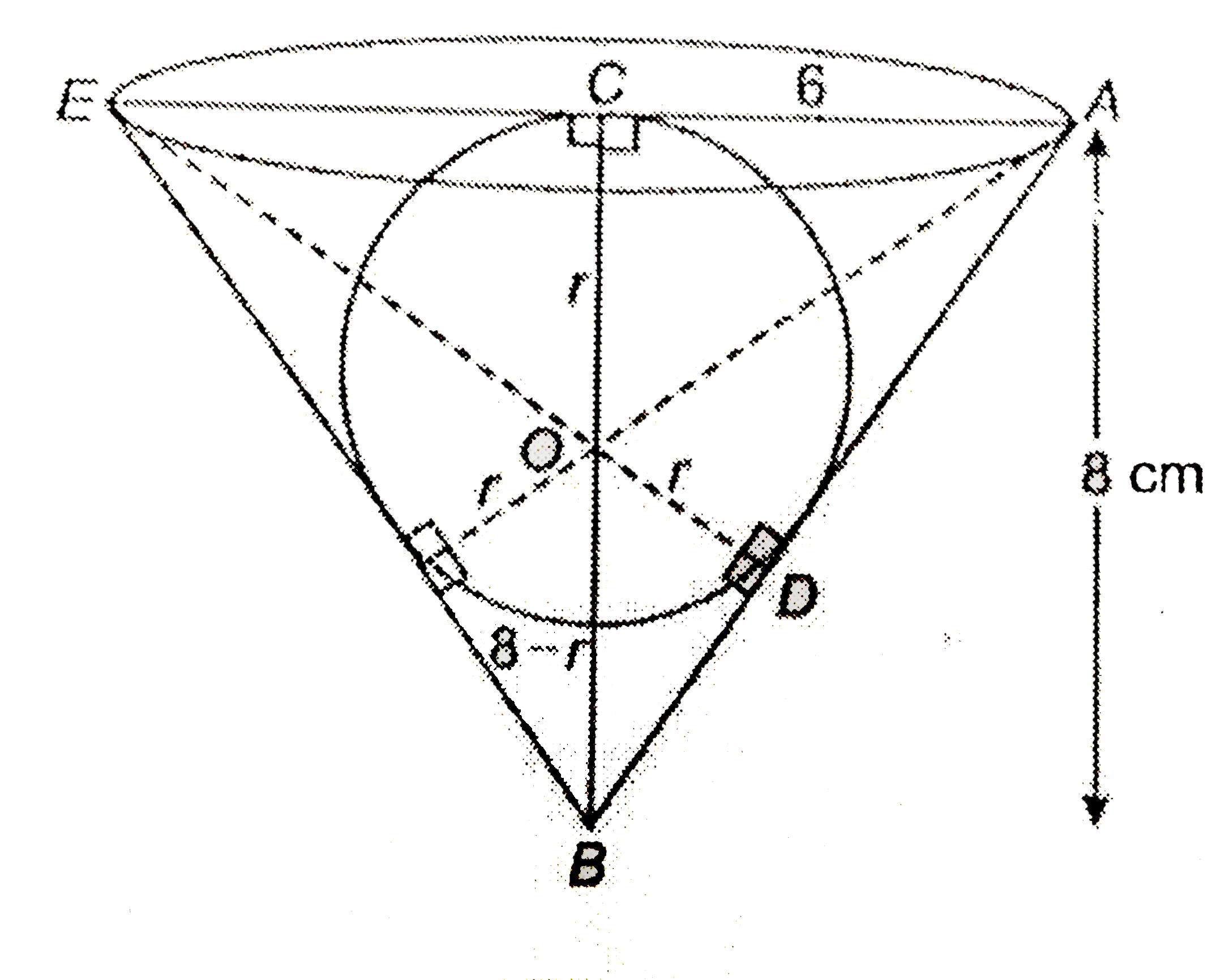
A conical vessel of radius 6 cm and height 8 cm is completely filled with water. a sphere is lowered into the water and its size is such that when it touches the the sides, it just immersed. what fraction of water overflows.

Video Solution

Text Solution

Verified by Experts

By Pythagoras theorem,
$A B^{2} = A C^{2} + C B^{2}$
$= {(6)}^{2} + {(8)}^{2} = {(10)}^{2}$
$\Rightarrow A B = \sqrt{100} = 10 c m$
Area of $Δ A B E = a r (Δ A O E) + a r (Δ E O B) + a r (Δ B O A)$
$= \frac{1}{2} \times 12 \times r + \frac{1}{2} \times 10 \times r + \frac{1}{2} \times 10 \times r$
= 16 r ......(1)
But $a r (Δ A B C) = \sqrt{s (s - a) (s - b) (s - c)}$ (where, $s = \frac{a + b + c}{2} = \frac{12 + 10 + 10}{2} = 16$ )
$\sqrt{16 (16 - 12) (16 - 10) (16 - 10)}$
$\sqrt{16 \times 4 \times 6 \times 6}$
$= 4 \times 2 \times 6$
$∴$ From (1) and (2), we have
$16 r = 4 \times 2 \times 6 \Rightarrow r = 3 c m$ .....(2)
Now, volume of water in the tank $= \frac{1}{3} π {(6)}^{2} \times 8$
Water overflows due to the sphere.
$∴$ Volume of water overflows = Volume of sphere $= \frac{4}{3} π {(3)}^{3}$
$∴$ Required fraction of water overflows $= \frac{\frac{4}{3} π {(3)}^{3}}{\frac{1}{3} π {(6)}^{2} \times 8} = \frac{3}{8}$

Updated on:21/07/2023

A cone of radius 3.5 cm and height 12 cm is completely filled with water. This water is emptied into an empty cylindrical vessel of radius 7 cm. What will be the height of water in this vessel ?
A2 cm
B0.33 cm
C0.5 cm
D1 cm
A cylindrical vessel of radius 8 cm contains water. A solid sphere of radius 6 cm is lowered into the water until it is completely immersed. What is the rise in the water level in the vessel?
A3 cm
B3.5 cm
C4 cm
D4.5 cm