A rod of length 12 cm moves with its ends always touching the coordinate axes. Determine the equation of the locus of a point P on the rod, which is 3cm from the end in contact with the x-axis.
Let the AB lies on axes OX and OY. P(x,y) be a moving point at 3 cm distance from A.
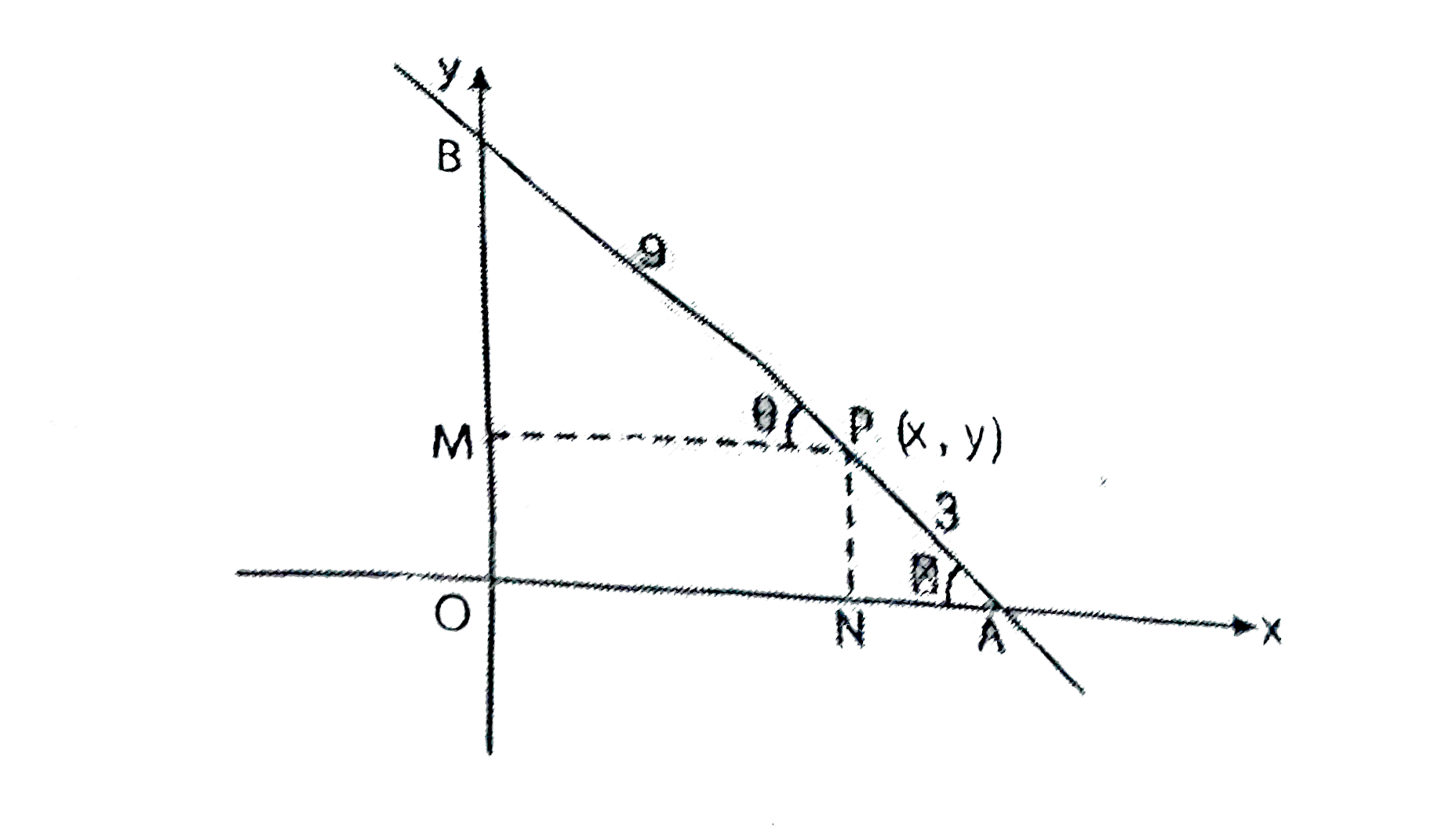
∴ BP=AB−AP=(12−3)cm=9cm
Let ∠(NAP)=∠(MPB)=θ
In ΔPMB, cosθ=x9
In ΔAPN, sinθ=y3
Now, from cos2θ+sin2θ=1
x281+y29=1 ⇒ x2+9y2=81
Topper's Solved these Questions
- CONIC SECTIONBook:NAGEEN PRAKASHANChapter:CONIC SECTIONExercise:Exercise 11.4
Explore 15 Videos
- COMPLEX NUMBERS AND QUADRATIC EQUATION Book:NAGEEN PRAKASHANChapter:COMPLEX NUMBERS AND QUADRATIC EQUATION Exercise:MISCELLANEOUS EXERCISE
Explore 20 Videos
- INTRODUCTION OF THREE DIMENSIONAL GEOMETRYBook:NAGEEN PRAKASHANChapter:INTRODUCTION OF THREE DIMENSIONAL GEOMETRYExercise:Miscellaneous Exercise
Explore 6 Videos
Similar Questions
A rod of length 12 cm moves with its ends always touching the coordinate axes. Determine the equation of the locus of a point P on the rod, which is 3 cm from the end in contact with the x–axis.
View SolutionA rod of length 12 cm moves with its ends always touching the coordinate axes. Determine the equation of the locus of a point P on the rod, which is 3cm from the end in contact with the x-axis.
View Solution
Knowledge Check
A line segment of 8 units in length moves so that its end points are always on the coordinate axes.Then, the equation of locus of its mid-point is
Ax2+y2=4Bx2+y2=16Cx2+y2=8D|x|+|y|=8
A rod AB of length 30 cm moves such that its ends always touching the co-ordinate axes. Determine the locus of a point C of the rod if AC : BC = 2 : 1
View SolutionA rod of length l cm moves with its ends A (on x=-axis) and B (on y-axis) always touching the coordinae axes. Prove that the point P on the rod which divides AB in the ratio λ(≠1) is ellipse. Alos, find the eccentricity of the ellipse.
View SolutionA straight rod of length 3l units slides with its ends A,B always on the x and y axes respectively,then the locus of the centriod of ΔOAB is
View SolutionA rod of length k slides in a vertical plane, its ends touching the coordinate axes. Prove that the locus of the foot of the perpendicular from the origin to the rod is (x2+y2)3=k2x2y2.
View SolutionThe ends of a rod of length l move on the co-ordinate axes. The locus of the point on the rod which divides it in the ratio 1:2 is
View SolutionA rod PQ of length 2a slides with its ends on the axes. The locus of the circumcentre of △OPQ is
View SolutionThe ends of a rod of length k moves on two positive coordinate axes.The locus of the point on the rod,which divides it in the ratio l:m is
View Solution