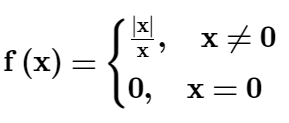If f(x) is defined as
$f (x) = {\begin{matrix} 2 x & + & 3 & x & \leq 0 3 x & + & 3 & x & \leq 0 \end{matrix}$
then evaluate : $lim x \to 0 f (x) and lim x \to 1 f (x)$

Video Solution

Answer

Step by step video & image solution for If f(x) is defined as f(x)={{:(2x,+,3,x,le 0),(3x,+,3,x,le0):} then evaluate : lim_(xrarr0) f(x) "and" lim_(xrarr1) f(x) by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.

Updated on:21/07/2023

Class 11 MATHS LIMITS AND DERIVATIVES

Topper's Solved these Questions

LIMITS AND DERIVATIVESBOOK - NAGEEN PRAKASHANCHAPTER - LIMITS AND DERIVATIVESEXERCISE - EX-13B
11 Videos
LIMITS AND DERIVATIVESBOOK - NAGEEN PRAKASHANCHAPTER - LIMITS AND DERIVATIVESEXERCISE - EX-13C
12 Videos
LIMITS AND DERIVATIVESBOOK - NAGEEN PRAKASHANCHAPTER - LIMITS AND DERIVATIVESEXERCISE - Miscellaneous Exercise
30 Videos
INTRODUCTION OF THREE DIMENSIONAL GEOMETRYBOOK - NAGEEN PRAKASHANCHAPTER - INTRODUCTION OF THREE DIMENSIONAL GEOMETRYEXERCISE - Miscellaneous Exercise
6 Videos
LINEAR INEQUALITIESBOOK - NAGEEN PRAKASHANCHAPTER - LINEAR INEQUALITIESEXERCISE - MISCELLANEOUS EXERCISE
14 Videos

Knowledge Check

Evaluate: $lim x \to 0 \frac{tan x - sin x}{x^{3}}$
A $1$
B $2$
C $\frac{1}{2}$
D $0$
If $f (x) = {\begin{matrix} 2 x + 3 & x \leq 0 3 (x + 1) & x > 0 \end{matrix}$ then the value of $lim x \to 0 f (x)$ is
A0
B6
C2
D3