A small mass m is attached to a massless string whose other end is fixed at P as shown in the figure. The mass is undergoing circular motion in the x-y plane with centre at O and constant angular speed ω. If the angular momentum of the system. calculated about O and P are denoted. by →LOand→LP respectively, then.

The correct Answer is:c
In figure, weight mg of the mass acts vertically downwards and tension T in the string acts along KP. Two rectangular components of T are Tcosθ opposite to mg and Tsinθ along KO.
About O, torque due to Tcosθ and mg cancel out. Torque due to Tsinθ is zero. Therefore, net torque about O is zero. As →τo=d→Lodt=0, ∴→LO= constant
i.e., →LO does not vary with time.
About P, torque due to T is zero, but torque due to mg ≠ 0
As →τp=d→LPdt≠0
∴→LP is not constant. It varies with time.

Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSBOOK - NCERT FINGERTIPSCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSEXERCISE - Equilibrium Of A Rigid Body
13 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSBOOK - NCERT FINGERTIPSCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSEXERCISE - Moment Of Inertia
7 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSBOOK - NCERT FINGERTIPSCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSEXERCISE - Motion Of Centre Of Mass
10 Videos
- PRACTICE PAPERSBOOK - NCERT FINGERTIPSCHAPTER - PRACTICE PAPERSEXERCISE - Practice Paper 3
50 Videos
- THERMAL PROPERTIES OF MATTERBOOK - NCERT FINGERTIPSCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Assertion And Reason
10 Videos
Similar Questions
A disc of mass M and radius R moves in the x-y plane as shown in the figure. The angular momentum of the disc at the instant shown is –
View SolutionTwo particles of mass m each are attached to a light rod of length d, one at its centre and the other at a free end, The rod is fixed at the other end is rotated in a plane at an angular speed ω. Calculate the angular momentum of the particle at the end with respect to the particle at the centre
View Solution
Knowledge Check
A small mass m is attached to a massless string whose other end is fixed at P as shown in the figure. The mass is undergoing circular motion in the x-y plane with centre at O and constant angular speed ω. If the angular momentum of the system. calculated about O and P are denoted. by vacLOandvacP respectively, then.
 A→LO and →LP do not vary with time.B→LO varies with time while →LP remains constantC→LO remains constant while →LP varies with timeD→LO and →LP both vary with time
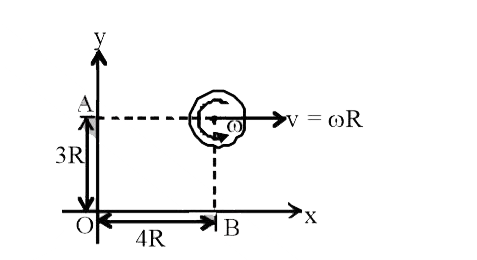
A→LO and →LP do not vary with time.B→LO varies with time while →LP remains constantC→LO remains constant while →LP varies with timeD→LO and →LP both vary with timeA particle is moving with constant speed v in xy plane as shown in figure. The magnitude of its angular velocity about point O is
 Av√a2+b2BvbCvb(a2+b2)Dva
Av√a2+b2BvbCvb(a2+b2)DvaA cube of mass m and side a is moving along a plane with constant speed vo as shown in figure. The magnitude of angular momentum of the cube about z -axis would be.
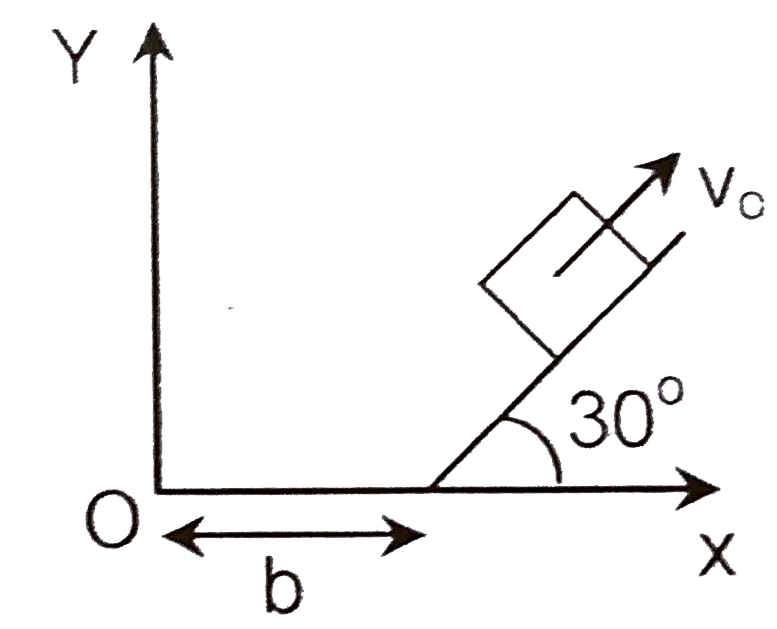 Amvob2B√3mvob2Cmvo(b−a2)DNone of these
Amvob2B√3mvob2Cmvo(b−a2)DNone of these
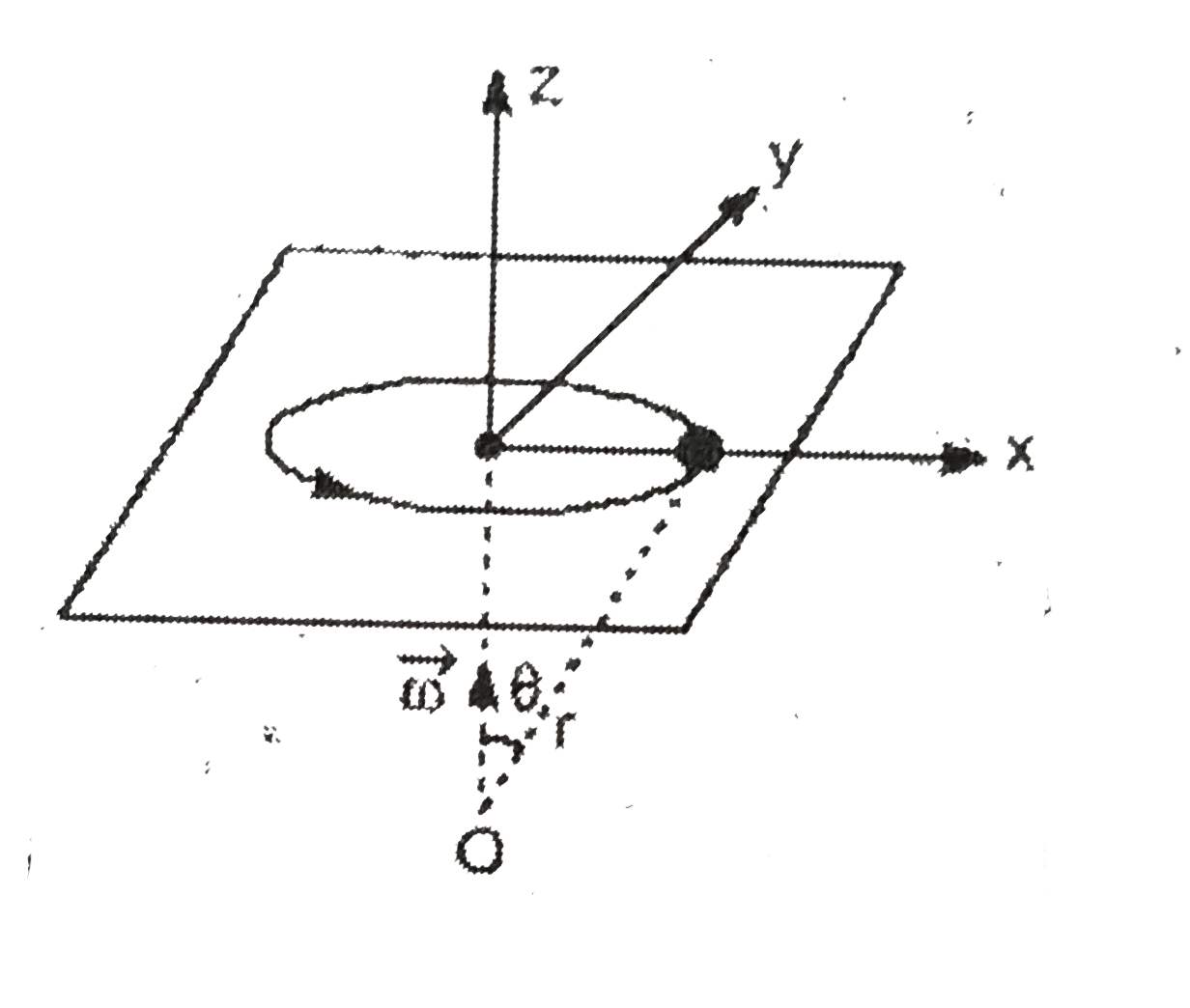
A mass m is attached to a rigid rod of negligible mass as shown in figure. The system is pivoted at point O and rotates about the indicated z-axis with angular velocity →ω, maintaining a fixed angle θ with the axis.
View SolutionTwo balls of masses m and 2m are attached to the ends of a light rod of length L. The rod rotates with an angular speed ω about an axis passing through the center of mass of system and perpendicular to the plane. Find the angular momentum of the system about the axis of rotation.
View SolutionA rod of mass m and length l is rotating about a fixed point in the ceiling with an angular velocity ω as shown in the figure. The rod maintains a constant angle θ with the vertical.
What is the rate of change of angular momentum of the rod ?

View SolutionA particle of mass m moves along line PC with velocity v as shown. What is the angular momentum of the particle about O?

View SolutionA particle of mass m moves along line PC with velocity v as shown. What is the angular momentum of the particle about O?

View Solution
