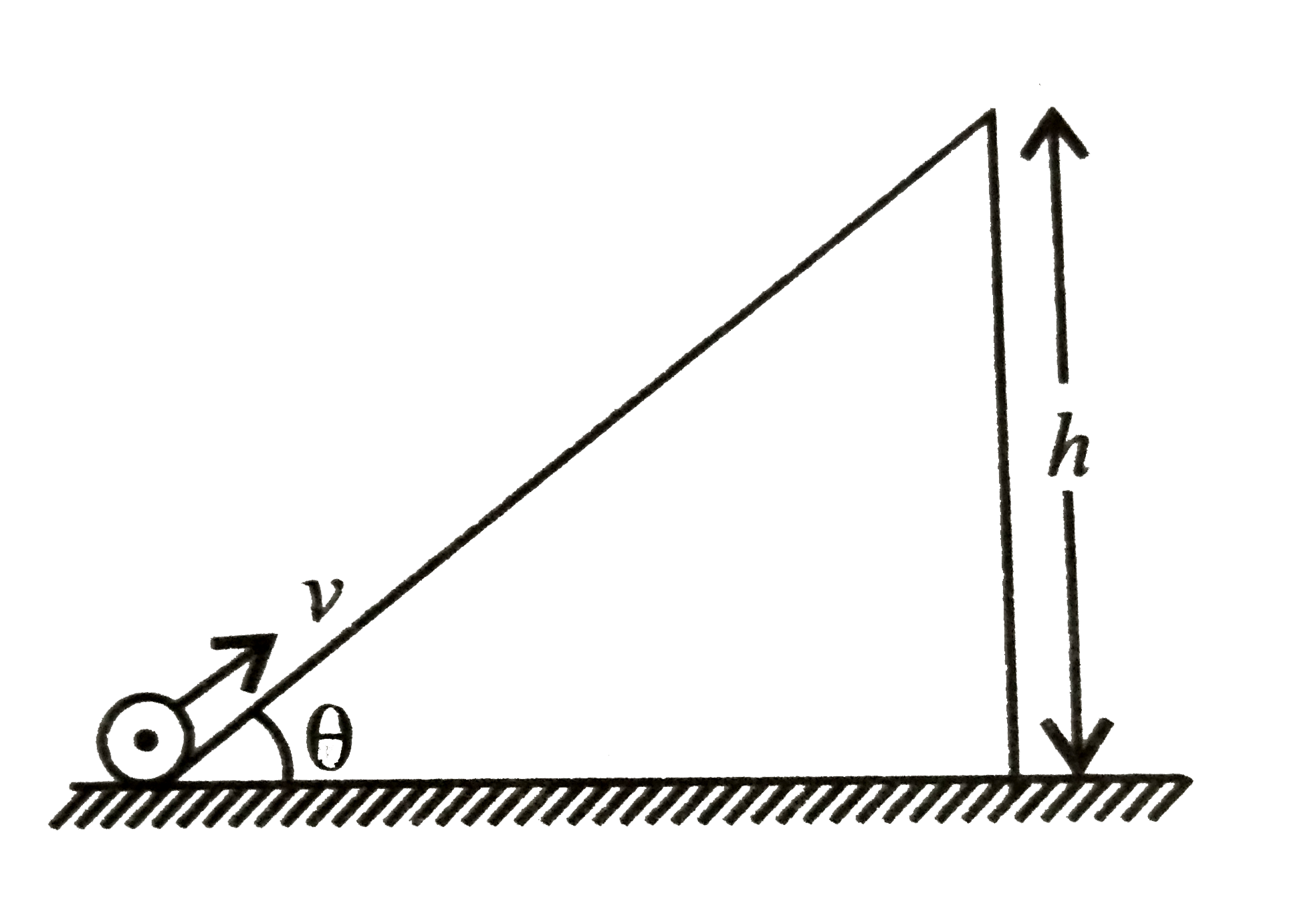
A solid cylinder rolls up an inclined plane of inclination $θ$ with an initial velocity $v$ . How far does the cylinder go up the plane ?

$\frac{3 v^{2}}{2 g sin θ}$

$\frac{v^{2}}{4 g sin θ}$

$\frac{3 v^{2}}{g sin θ}$

$\frac{3 v^{2}}{4 g sin θ}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

Updated on:21/07/2023

A solid cylinder roll up without slipping an inclined plane of inclination $θ$ with an initial velocity v. How for does the cylinder go up the plane :-
A $\frac{3 v^{2}}{2 g sin θ}$
B $\frac{v^{2}}{4 g sin θ}$
C $\frac{3 v^{2}}{g sin θ}$
D $\frac{3 v^{2}}{4 v sin θ}$
A solid cylinder is rolling down a rough inclined plane of inclination $θ$ . Then
AThe friction force is dissipative
BThe friction force is necessarily changing
CThe friction force will aid rotation but hinder translation
DThe friction force is reduced if $θ$ is reduced
If a solid cylinder rolls down an inclined plane, then its:
Arotational energy is $1 / 3$ and the translational energy $2 / 3$ of its total K.E.
Btranslational energy is $1 / 3$ and rotational energy is $2 / 3$ of its total K.E.
Crotational and translational energies are equal.
Dentire energy is rotational K.E.