From quantisation of angular momentum one gets for hydrogen atom, the radius of the nth orbit as rn=(n2me)(h2π)2(4π2ε0e2)
For a hydrogen like atom of atomic number Z,
A
the radius of the first orbit will be the same
B
rn will be greater for larger Z values
C
rn will be smaller for larger Z values
D
none of these
Text Solution
The correct Answer is:C
For an atom with a single electron, bohr atom model is applicable.
As the value of attraction between a proton and electron is proportional to e2, for an ion with a single electron, e24πε0 is replaced by Ze24πε0 i.e. rn∝n2Z.
|
Topper's Solved these Questions
- ATOMS BOOK - NCERT FINGERTIPSCHAPTER - ATOMS EXERCISE - The Line Spectra Of Hydrogen Atom
6 Videos
- ATOMS BOOK - NCERT FINGERTIPSCHAPTER - ATOMS EXERCISE - De Broglie Explanation Of Bohr Model
3 Videos
- ATOMS BOOK - NCERT FINGERTIPSCHAPTER - ATOMS EXERCISE - Atomic Spectra
19 Videos
- ALTERNATING CURRENT BOOK - NCERT FINGERTIPSCHAPTER - ALTERNATING CURRENT EXERCISE - Assertion And Reason
15 Videos
- COMMUNITCATION SYSTEMSBOOK - NCERT FINGERTIPSCHAPTER - COMMUNITCATION SYSTEMSEXERCISE - HOTS
10 Videos
Similar Questions
Knowledge Check
From quantisation of angular momentum one gets for hydrogen atom, the radius of the nth orbit as rn=(n2me)(h2π)2(4πε0e2)
For a hydrogen like atom of atomic number Z,Athe radius of the first orbit will be the sameBrn will be greater for larger Z valuesCrn will be smaller for larger Z valuesDnone of theseIn hydrogen atom, the radius of nth Bohr orbit is Vn. The graph Beetween log.(rnr1) will be
A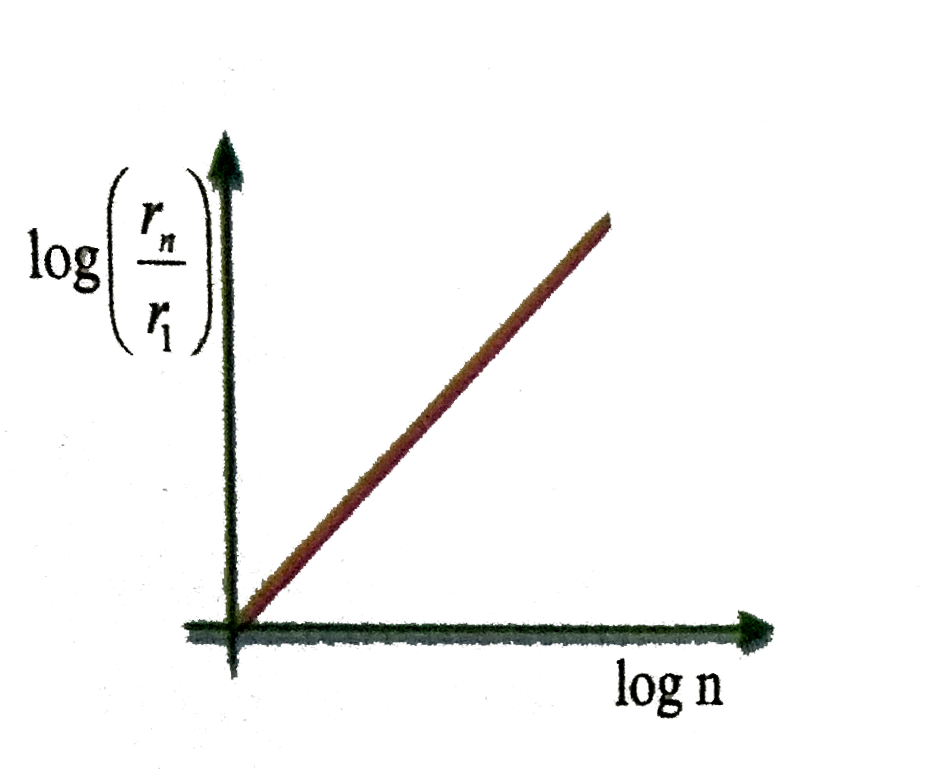 B
B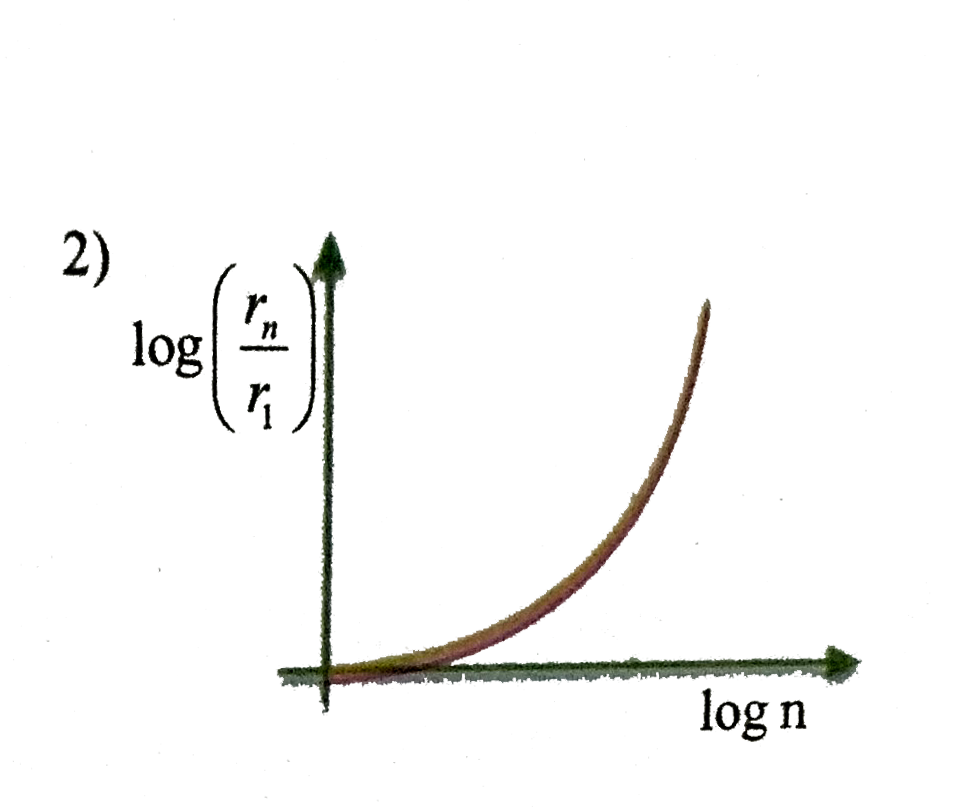 C
C D
D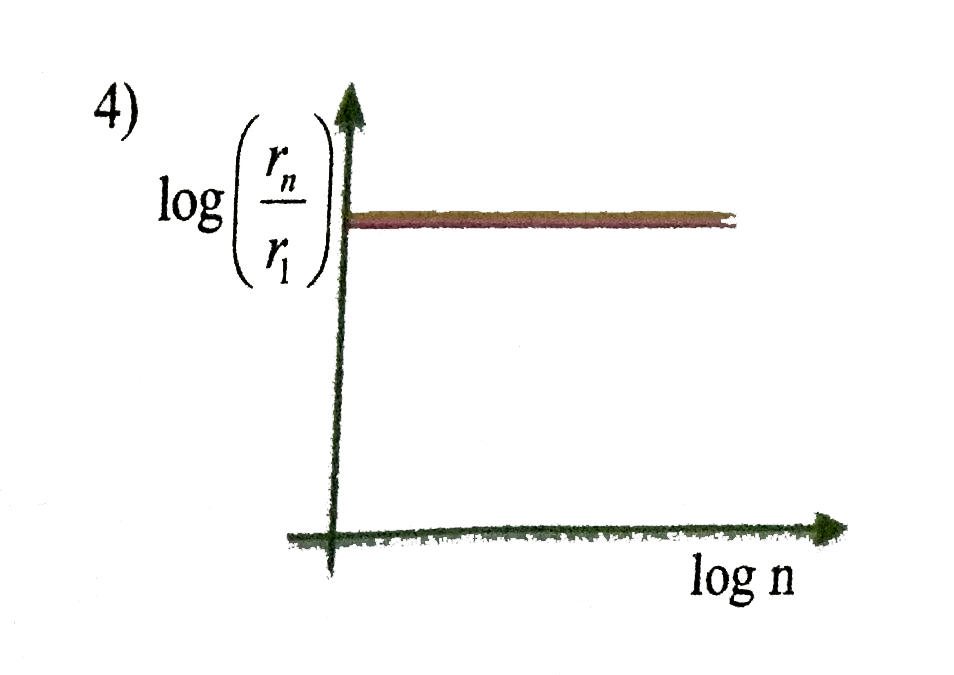
Assertion The radius of second orbit of hydrogen atom is 2.1Å
Reason Radius of nth orbit of hydrogen atom rn∝n2AIf both Assertion and Reason ar true and Reason is the correct explanation of Assertion.BIf both Assertion and Reason are true but Reason is not correct explanation of AssertionCIf Assertion is true by Reason is false.DIf Assertion is false but Reason is true.
Compute the angular momentum in 4th orbit, if L is the angular momentum of he electron in the 2nd orbit of hydrogen atom.
View SolutionCompute the angular momentum in 4th orbit, if L is the angular momentum of the electron in the 2nd orbit of hydrogen atom.
View SolutionWhen an electron jumps from n=4 to n=2 orbit in a hydrogen atom, we get,
View SolutionThe angular momentum J of the electron in a hydrogen atom is proportional to nth power of r (radius of the orbit) where n is :-
View SolutionEnergy of an electron in n th orbit of hydrogen atom is (k=14πε0)
View Solution
