(A) the trajetory traced by an incident particle depends on the impact parameter of collision.
(R) the impact parameter is the perpendicular distance of the initial velocity vector of the incident particle from the centre of the target nucleus.
if both assertion and reason are true and reason is the correct explanation of assertion.
if both assertion and reason are true but reason is not the correct explanation of assertion.
if assertion is true but reason is false.
if both assertion and reason are false.
The correct Answer is:B
NA
Topper's Solved these Questions
Similar Questions
Knowledge Check
In alpha-particle scattering experiment, the perpendicular distance(b) of initial velocity vector of the the alpha-particle from the centre of nucleus is equal to (where E is initial kinetic energy of alpha-particle) (##AAK_MCP_38_NEET_PHY_E38_020_Q01##)
AZe2sin2(θ2)4πε0EBZe2cot(θ2)4πε0ECZe2cos(θ2)4πε0EDZ2e2Esin4(θ2)4πε0Statement-1: Impact parameter for scattering of α particles by 180∘ is zero.
Statement-2 : Zero impact parameter means α particle tends to hit the centre of the nucleusAStatement-1 is true, Statement-2 is true and Statement-2 is correct explanation of Statement-1.BStatement-1 is true, Statement-2 is true, but Statement-2 is not a correct explanation of Statement-1.CStatement-1 is true, but Statement-2 is falseDStatement-1 is false, but Statement-2 is true.
A particle is projected with velocity u at angle θ with horizontal. Find the time when velocity vector is perpendicular to initial velocity vector.
View SolutionA particle is projected with velocity u at angle θ with horizontal. Find the time when velocity vector is perpendicular to initial velocity vector.
View SolutionWhat is the impact parameter at which the scattering angle is 10∘ for Z = 79 and initial energy of the α-particle is 5MeV ?
View SolutionWhat is the impact parameter for scattering of α-particle by 180∘?
View SolutionWhat is the impact parameter of an α-particle of initial energy 5 MeV scattered by 60∘ for Z=79 ?
View SolutionThere is a fixed sphere of radius R having positive charge Q uniformly spread in its volume. A small particle having mass m and negative charge (–q) moves with speed V when it is far away from the sphere. The impact parameter (i.e., distance between the centre of the sphere and line of initial velocity of the particle) is b. As the particle passes by the sphere, its path gets deflected due to electrostatics interaction with the sphere.
(a) Assuming that the charge on the particle does not cause any effect on distribution of charge on the sphere, calculate the minimum impact parameter b0 that allows the particle to miss the sphere. Write the value of b0 in term of R for the case
12mV2=100.(kQqR)
(b) Now assume that the positively charged sphere moves with speed V through a space which is filled with small particles of mass m and charge – q. The small particles are at rest and their number density is n [i.e., number of particles per unit volume of space is n].
The particles hit the sphere and stick to it. Calculate the rate at which the sphere starts losing its positive charge dQdt. Express your answer in terms of b0
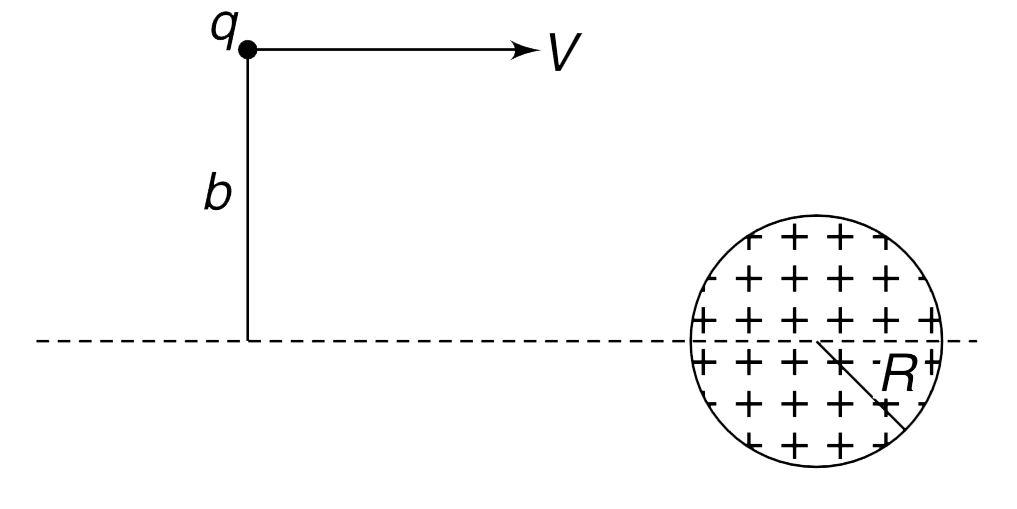
View Solution
