Mercury is completely filled in a rectangular take of height 72 cm. The atmospheric pressure at the place is 72 cm. of Hg. Find the distance in cm of point of application from bottom of tank of the net force , on the inner surface of the side vertical wall of tank.
32 cm
16 cm
74 cm
42 cm
The correct Answer is:A
To solve the problem, we need to find the distance from the bottom of the tank to the point of application of the net force on the inner surface of the vertical wall of the tank filled with mercury. Here’s a step-by-step solution:
Step 1: Understand the Problem
We have a rectangular tank filled with mercury to a height of 72 cm. The atmospheric pressure at this location is also equivalent to 72 cm of mercury. We need to find the distance from the bottom of the tank to the point where the net force acts on the vertical wall.
Step 2: Define the Variables
- Height of the mercury column (h) = 72 cm
- Atmospheric pressure (P₀) = 72 cm of Hg
- Density of mercury (ρ) = 13.6 g/cm³ (or 13600 kg/m³ in SI units)
- Acceleration due to gravity (g) = 9.81 m/s²
Step 3: Calculate the Pressure at Depth
The pressure at a depth x in the fluid can be calculated using the formula:
P=P₀+ρgh
Where:
- P₀ is the atmospheric pressure (72 cm of Hg converted to cm of water).
- ρ is the density of mercury.
- g is the acceleration due to gravity.
- h is the height of the mercury column.
Step 4: Average Pressure on the Wall
To find the average pressure on the wall, we need to consider the pressure at the top and bottom of the tank:
- At the top (x = 0): P=P₀=72cm Hg
- At the bottom (x = 72 cm): P=P₀+ρgh
The average pressure (P_avg) can be calculated as:
Pavg=Ptop+Pbottom2
Step 5: Calculate the Total Force on the Wall
The total force (F) acting on the wall can be calculated using:
F=Pavg×A
Where A is the area of the wall. If we assume the width of the tank is B, then:
A=h×B=72cm×B
Step 6: Calculate the Torque
To find the point of application of the force, we need to calculate the torque about the bottom of the tank. The torque (τ) due to the pressure on a differential strip at height x can be expressed as:
dτ=P(x)⋅A⋅x
Integrating this from 0 to 72 cm will give us the total torque.
Step 7: Find the Point of Application
The point of application of the force can be found by setting the total torque equal to the torque due to the average force acting at a distance y from the bottom:
F⋅y=τ
Step 8: Solve for y
Rearranging gives:
y=τF
Step 9: Calculate the Distance from the Bottom
Finally, the distance from the bottom of the tank to the point of application of the net force is:
Distance from bottom=72cm−y
Final Answer
After performing the calculations, we find that the distance from the bottom of the tank to the point of application of the net force is 32 cm.
---
We have a rectangular tank filled with mercury to a height of 72 cm. The atmospheric pressure at this location is also equivalent to 72 cm of mercury. We need to find the distance from the bottom of the tank to the point where the net force acts on the vertical wall.
- Height of the mercury column (h) = 72 cm
- Atmospheric pressure (P₀) = 72 cm of Hg
- Density of mercury (ρ) = 13.6 g/cm³ (or 13600 kg/m³ in SI units)
- Acceleration due to gravity (g) = 9.81 m/s²
The pressure at a depth x in the fluid can be calculated using the formula:
P=P₀+ρgh
Where:
- P₀ is the atmospheric pressure (72 cm of Hg converted to cm of water).
- ρ is the density of mercury.
- g is the acceleration due to gravity.
- h is the height of the mercury column.
To find the average pressure on the wall, we need to consider the pressure at the top and bottom of the tank:
- At the top (x = 0): P=P₀=72cm Hg
- At the bottom (x = 72 cm): P=P₀+ρgh
Pavg=Ptop+Pbottom2
The total force (F) acting on the wall can be calculated using:
F=Pavg×A
Where A is the area of the wall. If we assume the width of the tank is B, then:
A=h×B=72cm×B
To find the point of application of the force, we need to calculate the torque about the bottom of the tank. The torque (τ) due to the pressure on a differential strip at height x can be expressed as:
dτ=P(x)⋅A⋅x
Integrating this from 0 to 72 cm will give us the total torque.
The point of application of the force can be found by setting the total torque equal to the torque due to the average force acting at a distance y from the bottom:
F⋅y=τ
Rearranging gives:
y=τF
Finally, the distance from the bottom of the tank to the point of application of the net force is:
Distance from bottom=72cm−y
After performing the calculations, we find that the distance from the bottom of the tank to the point of application of the net force is 32 cm.
Topper's Solved these Questions
Similar Questions
A vertical cylinder of height 100cm contains air at a constant temperature. The top is closed by a friction less light piston. The atmospheric pressure is equal to 75 cm of mercury. Mercury is slowly poured over the piston. Find the maximum height of the mercury column that can be put on the piston.
View SolutionWater is filled in a rectangular tank of size 3m×2m×1m. a. Find the total force exerted by the water on the bottom surface of the tank. b. cosider a vertical side of area 2m×1m. Take a horizontal strip of wide δx metre in this side, situated at a depth of x metre from the surface of water. Find the torque of the force calculate in part b. about the bottom edge of this side. e. Find the total torque by the water on the side about the bottom edge. neglect the atmospheric pressure and take =10ms−2.
View Solution
Knowledge Check
The volume of an air bubble becomes three times as it rises from the bottom of a lake to its surface. Assuming atmospheric pressure to be 75 cm of Hg and the density of water to be 1/10 of the density of mercury, the depth of the lake is
A5mB10mC15mD20mA tank of height 33.25 cm is completely filled with liquid (μ = 1.33). An object is placed at the bottom of tank on the axis of concave mirror as shown in the figure. Image of the object is formed 25 cm below the surface of the liquid, then focal length of the mirror is
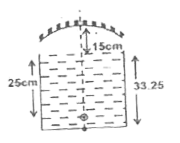 A10 cmB15 cmC20cmD25 cm
A10 cmB15 cmC20cmD25 cmThe volume of an air bubble is doubled as it rises from the bottom of lake to its surface, The atmospheric pressure is 75 cm of mercury. The ratio of density of mercury to that of lake water is 4030, the depth of the lake in metre is
A15B10C30D20
The image of a candle flame placed at a distance of 30 cm from a spherical lens is formed on a screen placed on the other side of the lens at a distance of 60 cm from the optical centre of the lens. Identify the type of lens and calculate its focal length. If the height of the flame is 3 cm, find the height of its image.
View SolutionA convex lens is held 45cm above the bottom of an empty tank. The image of a point at the bottom of a tank is formed 36cm above the lens. Now, a liquid is poured into the tank to a depth of 40cm. It is found that the distance of the image of the same point on the bottom of the tank is 48cm above the lens. Find the refractive index of the liquid.
View SolutionA tank of square cross-section of each side is filled with a liquid of height h . Find the thrust experienced by the vertical surfaces and bottom surface of the tank.
View SolutionIf an air bubbles rises from the bottom of a mercury tank to the top its volume becomes 112 times. When normal pressure is 76cm of Hg then the depth of the Hg tank is
View SolutionTwo holes are made in the side of the tank such that the jets of water flowing out of them meet at the same point on the ground. If one hole is at a height of 3cm above the bottom, then the distance of the other holes from the top surface of water is
View Solution
