A beam of light is travelling from region II to region III (see the figure) . The refractive index in the region I,II and III are n0,n0√2,andn02 respectively . The angle of incidence θ for which the beam just misses entering region III is
30∘
45∘
60∘
sin−1√2
The correct Answer is:A
To solve the problem, we need to determine the angle of incidence θ for which a beam of light traveling from region II to region III just misses entering region III. This situation corresponds to the condition for total internal reflection at the boundary between regions II and III.
1. Identify the refractive indices:
- Let the refractive index of region I be n0.
- The refractive index of region II is n0√2.
- The refractive index of region III is n02.
2. Determine the critical angle:
- The critical angle θc for total internal reflection occurs when light travels from a medium with a higher refractive index (region II) to a medium with a lower refractive index (region III).
- The formula for the critical angle is given by:
sinθc=n3n2
- Substituting the values:
sinθc=n02n0√2=1√2
- Therefore, θc=45∘.
3. Apply Snell's Law at the boundary between region I and region II:
- At the boundary between region I (with refractive index n0) and region II (with refractive index n0√2), we apply Snell's Law:
n1sinθ=n2sinθc
- Substituting the known values:
n0sinθ=n0√2sin45∘
- Since sin45∘=1√2, we have:
n0sinθ=n0√2⋅1√2=n02
4. Solve for sinθ:
- Dividing both sides by n0:
sinθ=12
5. Calculate θ:
- The angle θ can be found using the inverse sine function:
θ=sin−1(12)=30∘
Thus, the angle of incidence θ for which the beam just misses entering region III is 30∘.
- Let the refractive index of region I be n0.
- The refractive index of region II is n0√2.
- The refractive index of region III is n02.
- The critical angle θc for total internal reflection occurs when light travels from a medium with a higher refractive index (region II) to a medium with a lower refractive index (region III).
- The formula for the critical angle is given by:
sinθc=n3n2
- Substituting the values:
sinθc=n02n0√2=1√2
- Therefore, θc=45∘.
- At the boundary between region I (with refractive index n0) and region II (with refractive index n0√2), we apply Snell's Law:
n1sinθ=n2sinθc
- Substituting the known values:
n0sinθ=n0√2sin45∘
- Since sin45∘=1√2, we have:
n0sinθ=n0√2⋅1√2=n02
- Dividing both sides by n0:
sinθ=12
- The angle θ can be found using the inverse sine function:
θ=sin−1(12)=30∘
Topper's Solved these Questions
Similar Questions
A ray of light is incident on the left vertical face of glass cube of refractive index n2, as shown in figure. The plane of incidence is the plane of the page, and the cube is surrounded by liquid (refractive index=n1). What is the largest angle of incidence θ1 for which total internal reflection occurs at the top surfaces?

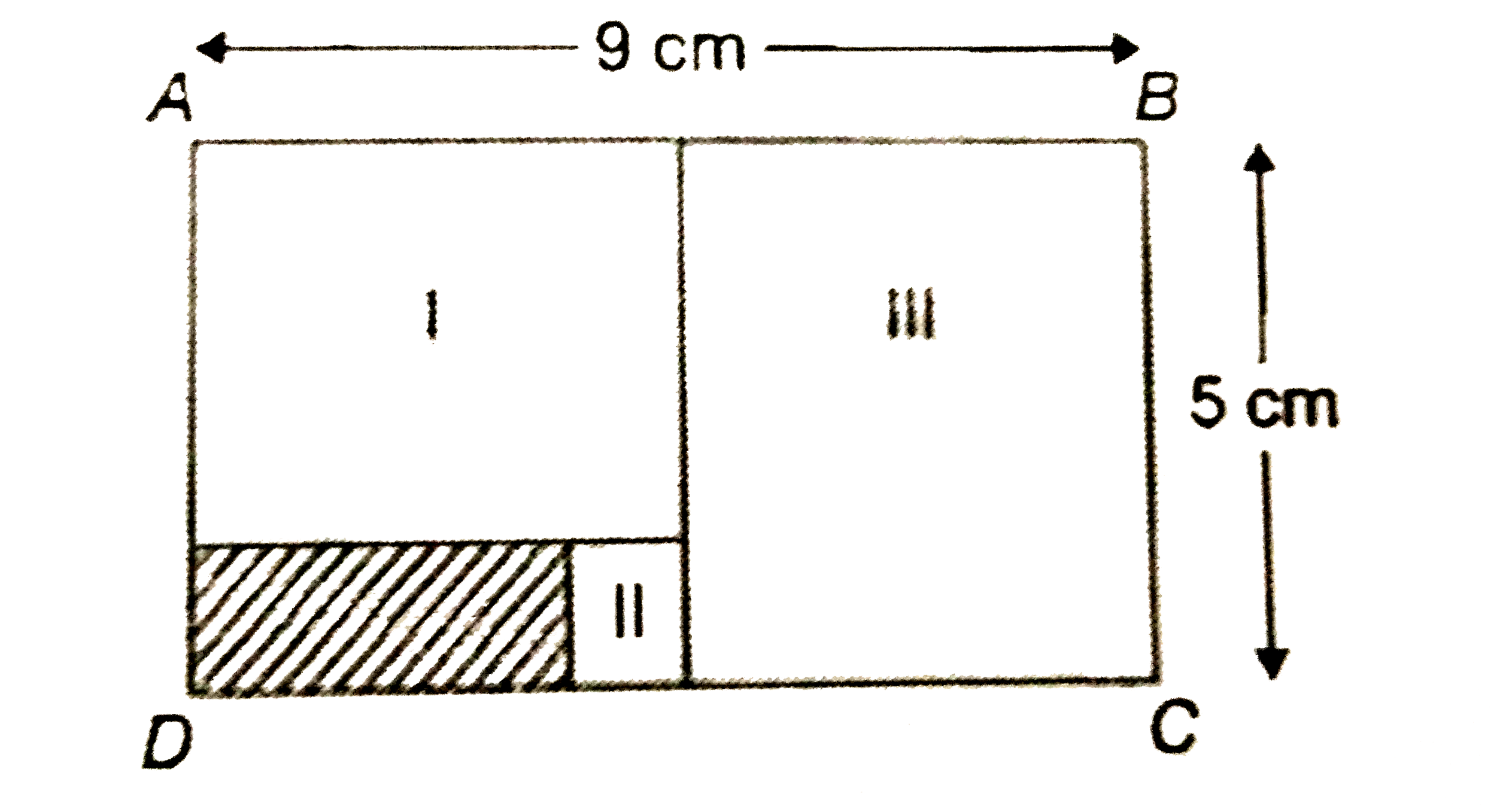
View SolutionIn the given figure, ABCD is a rectangle I,II and III are squares. Find the area of the shaded region.
View Solution
Knowledge Check
A light beam is travelling from Region I to IV (figure). The refractive index in regionals I,II,III and IV are n0=n02(n_0)/(6) and (n_0)/(8)respectively.The∠of∈cncethetaforwhichthebeamjustmissesenter∈gregionIVis−
 Asin−1(34)Bsin−1(18)Csin−1(14)Dsin−1(13)
Asin−1(34)Bsin−1(18)Csin−1(14)Dsin−1(13)A light beam is traveling from Region I to region IV (refer figure). The refractive indices in Region I, II, III, and IV are n0,n0/2,n0/6andn0/8 , respectively. The angle of incidence θ for which the beam just misses entering Region IV is
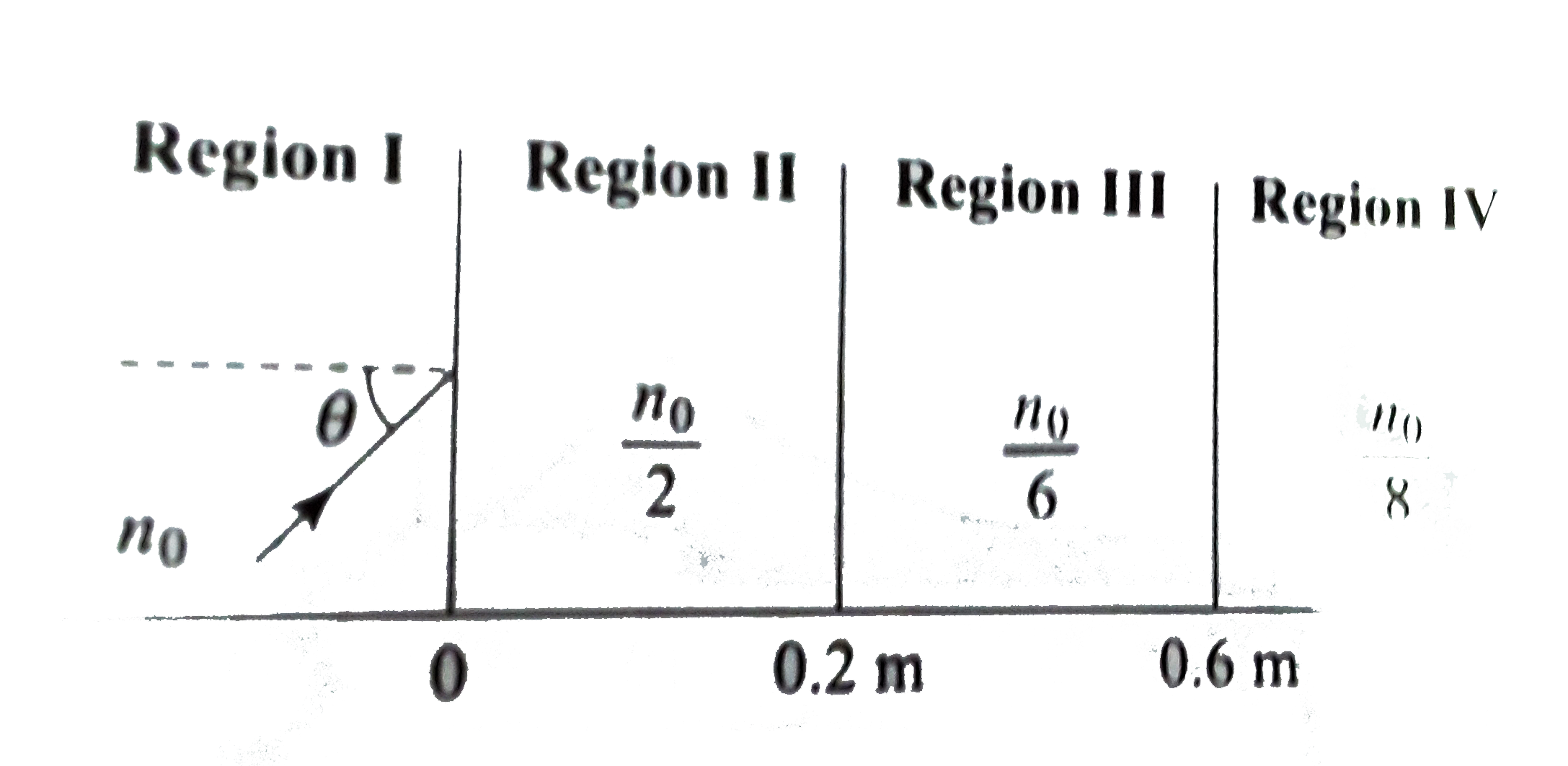 Asin−1(3/4)Bsin−1(1/8)Csin−1(1/4)Dsin−1(1/3)
Asin−1(3/4)Bsin−1(1/8)Csin−1(1/4)Dsin−1(1/3)The refractive index of the material of the prism for a monochromatic beam of light is 2 and its refracting angle is 60∘ . The angle of incidence corresponding to which this beam of light suffers minimum deviation is :
A30∘B45∘C60∘D75∘
The refractive index of water is 4/3 and that of glass is 3/2. A beam of light enters glass from water. For what angle of incidence will the refracted light be completely polarised ?
View SolutionA ray of light goes from a medium of refractive index n1 to a medium of refractive index n2. The angle of incidence is I and the angle of refraction is r. Then, sin i/sin r is equal to
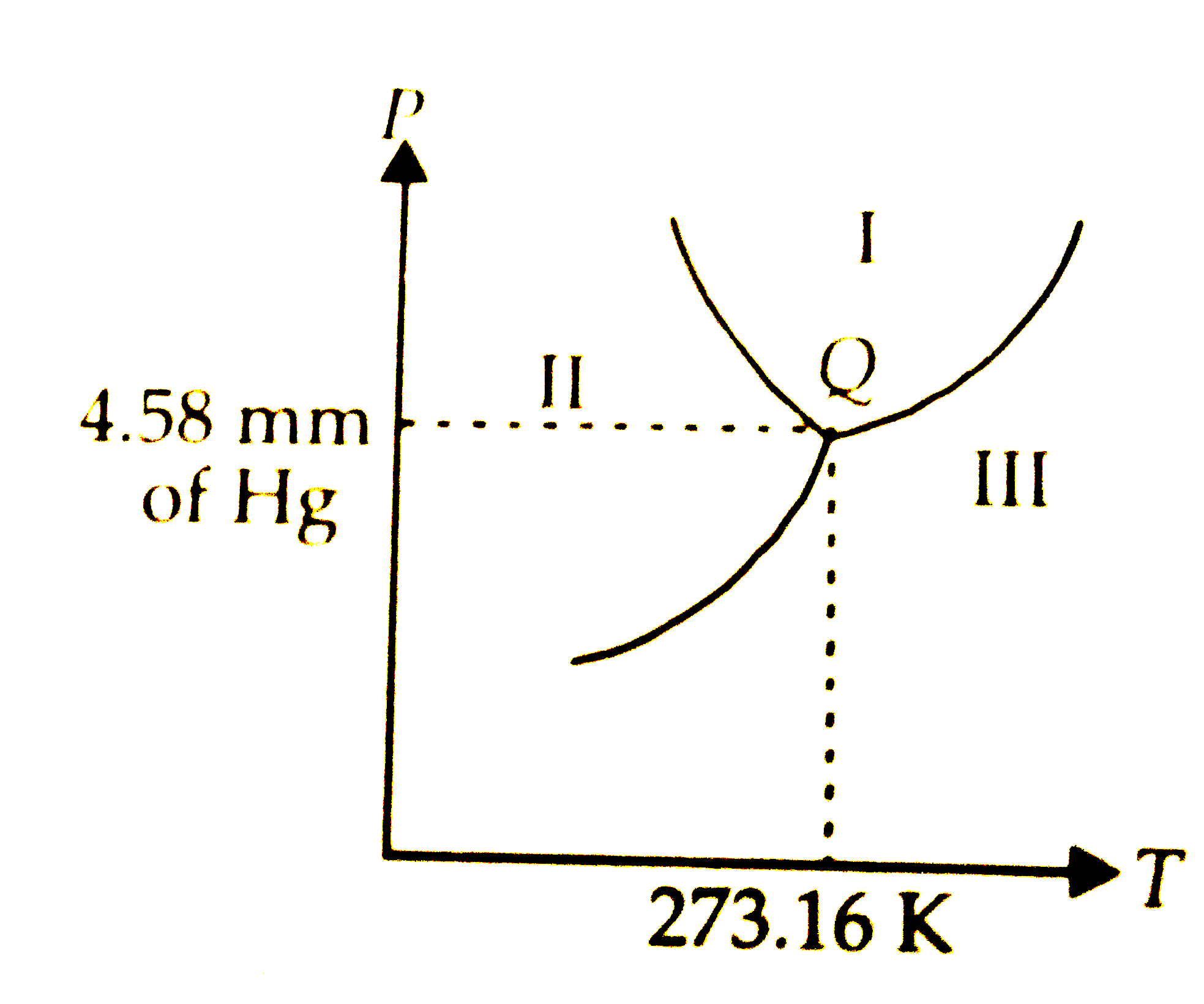
View SolutionIn the phase diagram showns, the point Q corresponds to the triple point of water. The region I, II and III respectively correspond to phases
View SolutionA ray of light travels from a medium of refractive index n1 to
a medium of refractive index n2. If angle of incidence is i and
angle of refraction is r, than sinisinr is equal to
View SolutionA beam of light propagating in medium A with index of refraction n(A) passes across an interface into medium B with index of refraction n(B). If v(A) and v(B) are the speeds of light in A and B respectively. Then which of the following is true?
View Solution
