A simple spring has length l and force constant K. It is cut into two springs of lengths l1andl2 such that l1=nl2 (n = an integer). The force constant of spring of length l1 is
knn+1
k(n+1)n
k(n−1)n
knn−1
The correct Answer is:B
Step by step video, text & image solution for A simple spring has length l and force constant K. It is cut into two springs of lengths l_(1) "and" l_(2) such that l_(1) = n l_(2) (n = an integer). The force constant of spring of length l_(1) is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A spring of force constant k is cut into two pieces of lengths l1 and l2. Calculate force constant of each part.
View SolutionA uniform spring whose unstretched length is l has a force constant k. the spring is cut into two pieces of unstretched lengths l1 and l2, where l1=nl2 and n is an integer. What are the corresponding force constant k1 and k2 in terms of n and k? what is the ratio k1/k2
View Solution
Knowledge Check
A spring has length'l' and spring constant 'k'. It is cut into two pieces of lengths l1andl2 such that l1=nl2. The force constant of the spring of length l1 is
Ak(l+n)BkCk(n+1)Dk(n+l)nA spring has length l and force constant k it is cut into two springs of legnth l1 and l2 such that l1=nl2(n=an integer). Mass 'm' suspended form l1 oscillates with time period.
AT=2π√m(n+1)KBT=2π√nm(n+1)KCT=2π√mKDT=2π√(n+1)mKA uniform spring whose unstressed length is l has a force constant k. The spring is cut into two pieces of unstressed lengths l1 and l2 where l1=nl2 where n being on integer. Now a mass m is made to oscillate with first spring. The time period of its oscillation would be
AT=2π√mnk(n+1)BT=2π√mk(n+1)CT=2π√mkDT=2π√m(n+1)nk
The length of wire, when M1 is hung from it, is l1 and is l2 with both M1 and M2 hanging. The natural length of wire is :-
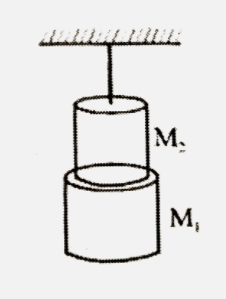
View SolutionA spring of length 'l' has spring constant 'k' is cut into two parts of length l1 and l2. If their respective spring constahnt are K1 and k2, then K1K2 is:
View SolutionA spring of force constant k is cut into two pieces whose lengths are in the ratio 1:2. The force constant of the longer piece?
View SolutionA spring of certain length and having spring constant k is cut into two pieces of length in a ratio 1:2. The spring constants of the two pieces are in a ratio :
View SolutionA string of length L and force constant k is stretched to obtain extension l. It is further stretched to obtain extension l1. The work done in second streching is
View Solution