Find the displacement equation of the simple harmonic motion obtained by conbining the motions.
x1=2sin ωt,x2=4sin (ωt+π6)
and x3=6sin(ωt+π3)
x=10.25sin(ωt+ϕ)
x=10.25sin(ωt−ϕ)
x=11.25sin(ωt+ϕ)
x=11.25sin(ωt−ϕ)
The correct Answer is:C
Step by step video, text & image solution for Find the displacement equation of the simple harmonic motion obtained by conbining the motions. x_(1)=2 "sin "omegat,x_(2)=4 "sin "(omegat+(pi)/(6)) and x_(3)=6 "sin" (omegat+(pi)/(3)) by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
Choose the most appropriate option.
What will be the displacement equation, of the simple harmonic motion obtained by combining the motions?
x1=2sinωt,x2=4sin(ωt+π6)
x3=6sin(ωt+π3)Ax=10.25sin(ωt+ϕ)Bx=10.25sin(ωt−ϕ)Cx=11.25sin(ωt+ϕ)Dx=11.25sin(ωt−ϕ)Find the resultant amplitude of the following simple harmonic equations :
x1=5sinωt
x2=5sin(ωt+53∘)
x3=−10cosωtA5B10C15D20What is the phase difference between two simple harmonic motions represented by x1=Asin(ωt+π6) and x2=Acosωt?
Aπ6Bπ3Cπ2D2π3
Find the amplitude of the harmonic motion obtained by combining the motions
x1=(2.0cm)sinωt
and x2=(2.0cm)sin(ωt+π/3).
View SolutionIf current 11=3A sin ωtand12=4Acosωt,then13 is
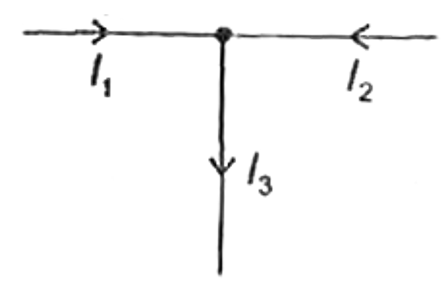
View SolutionUsing graphical means find an amplitude a of oscillations resulting from the superposition of the following oscillations of the same direction :
(a)x1=3.0cos(ωt+π/3),x2=8.0sin(ωt+π/6),
(b) x1=3.0cosωt,x2=5.0cos(ωt+π/4),x3=6.0sinωt.
View SolutionWhat is the phase difference between two simple harmonic motions represented by x1=Asin(ωt+π6) and x2=Acos(ωt)?
View SolutionThe displacement equation of a simple harmonic oscillator is given by y=Asinωt−Bcosωt
The amplitude of the oscillator will be
View Solution
