If a small sphere of mass m and charge q is hanged from a silk thread at an angle θ with the surface of a vectical charged conductinb plate, then for equilibrium of sphere the surface charge density of the plate -
ε0mgtanθq
(2ε0mgtanθ)/q
ε0mgqtanθ
ε0mgtanθ3q
The correct Answer is:B
To solve the problem of finding the surface charge density of a vertical charged conducting plate that keeps a small sphere of mass m and charge q in equilibrium at an angle θ, we can follow these steps:
Step 1: Understand the Forces Acting on the Sphere
The sphere experiences three main forces:
1. The gravitational force →Fg=mg acting downward.
2. The tension force →T in the thread, which acts at an angle θ to the vertical.
3. The electric force →Fe=qE due to the electric field E created by the charged plate.
Step 2: Resolve the Tension Force
The tension T can be resolved into two components:
- The vertical component: Tcosθ=mg
- The horizontal component: Tsinθ=qE
Step 3: Calculate the Electric Field
For an infinite charged conducting plate, the electric field E due to the surface charge density σ is given by:
E=σ2ϵ0
where ϵ0 is the permittivity of free space.
Step 4: Substitute Electric Field into the Horizontal Force Equation
From the horizontal component of the tension, we have:
Tsinθ=qE
Substituting for E:
Tsinθ=q(σ2ϵ0)
Step 5: Substitute Tension from the Vertical Force Equation
From the vertical component of the tension, we have:
T=mgcosθ
Substituting this into the horizontal force equation gives:
mgcosθsinθ=q(σ2ϵ0)
Step 6: Simplify the Equation
This simplifies to:
mgtanθ=qσ2ϵ0
Step 7: Solve for Surface Charge Density σ
Rearranging the equation to solve for σ:
σ=2ϵ0mgtanθq
Final Result
Thus, the surface charge density σ of the plate is given by:
σ=2ϵ0mgtanθq
The sphere experiences three main forces:
1. The gravitational force →Fg=mg acting downward.
2. The tension force →T in the thread, which acts at an angle θ to the vertical.
3. The electric force →Fe=qE due to the electric field E created by the charged plate.
The tension T can be resolved into two components:
- The vertical component: Tcosθ=mg
- The horizontal component: Tsinθ=qE
For an infinite charged conducting plate, the electric field E due to the surface charge density σ is given by:
E=σ2ϵ0
where ϵ0 is the permittivity of free space.
From the horizontal component of the tension, we have:
Tsinθ=qE
Substituting for E:
Tsinθ=q(σ2ϵ0)
From the vertical component of the tension, we have:
T=mgcosθ
Substituting this into the horizontal force equation gives:
mgcosθsinθ=q(σ2ϵ0)
This simplifies to:
mgtanθ=qσ2ϵ0
Rearranging the equation to solve for σ:
σ=2ϵ0mgtanθq
Thus, the surface charge density σ of the plate is given by:
σ=2ϵ0mgtanθq
Topper's Solved these Questions
Similar Questions
To what potential, must we charge an insulated sphere of radius 14 cm so that its surface charge density of 1μCm−2 ?
View SolutionTwo small spheres each of mass m and charge q are tied from the same rigid support with the help of silk threads of length L. They make angle θ with the vertical as shown in the fig. If length L is decreased, then angle θ with the vertical.
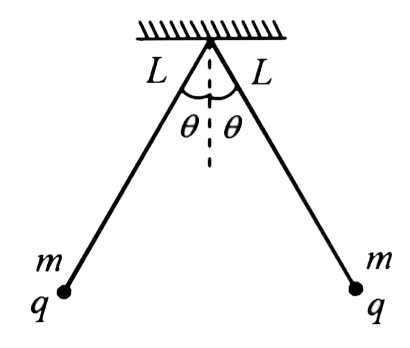
View Solution
Knowledge Check
If a small sphere of mass m and charge q is hung from a silk thread at an angle θ with the surface of a vertical charged conducting plate, then for equilibrium of sphere, the surface charge density of the plate is
Aε0(mgq)tanθBε0(2mgq)tanθCε0(mgq)tanθDε0(mg3q)tanθA point object of mass 1mg and charge 1μC is hung with a silk thread at an angle 45 with the surface of a vertical uniformly charged conducting plate. For equilibrium of object , the surface charge density (in SI unit) of the plate is (g= 10m/s2)
A104ε0√3B104ε0C10ε0√3D10ε0A charged ball B hangs from a silk thread S, which makes an angle θ with a large charged conducting sheet P, as shown in figure. The surface charge density σ of the sheet is proportional to
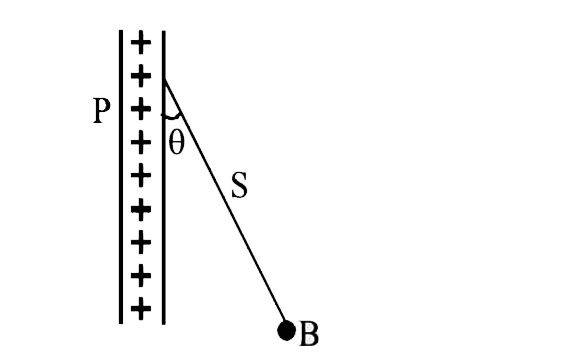 A(a) cotθB(b) cosθC(c) tanθD(d) sinθ
A(a) cotθB(b) cosθC(c) tanθD(d) sinθ
At which of the two points, 1 or 2, of a charged capacitor with nonparallel plates is the surface charge density greater?
View SolutionTo what potential we must charge an insulate sphere of radius 14 cm, so that the surface charge density is equal to 2μCm−2 ?
View SolutionA charged ball B hangs from a silk thread S, which makes an angle θ with a large charged conducting sheet P, as shown in the figure. The surface charge density σ of the sheet is proportional to
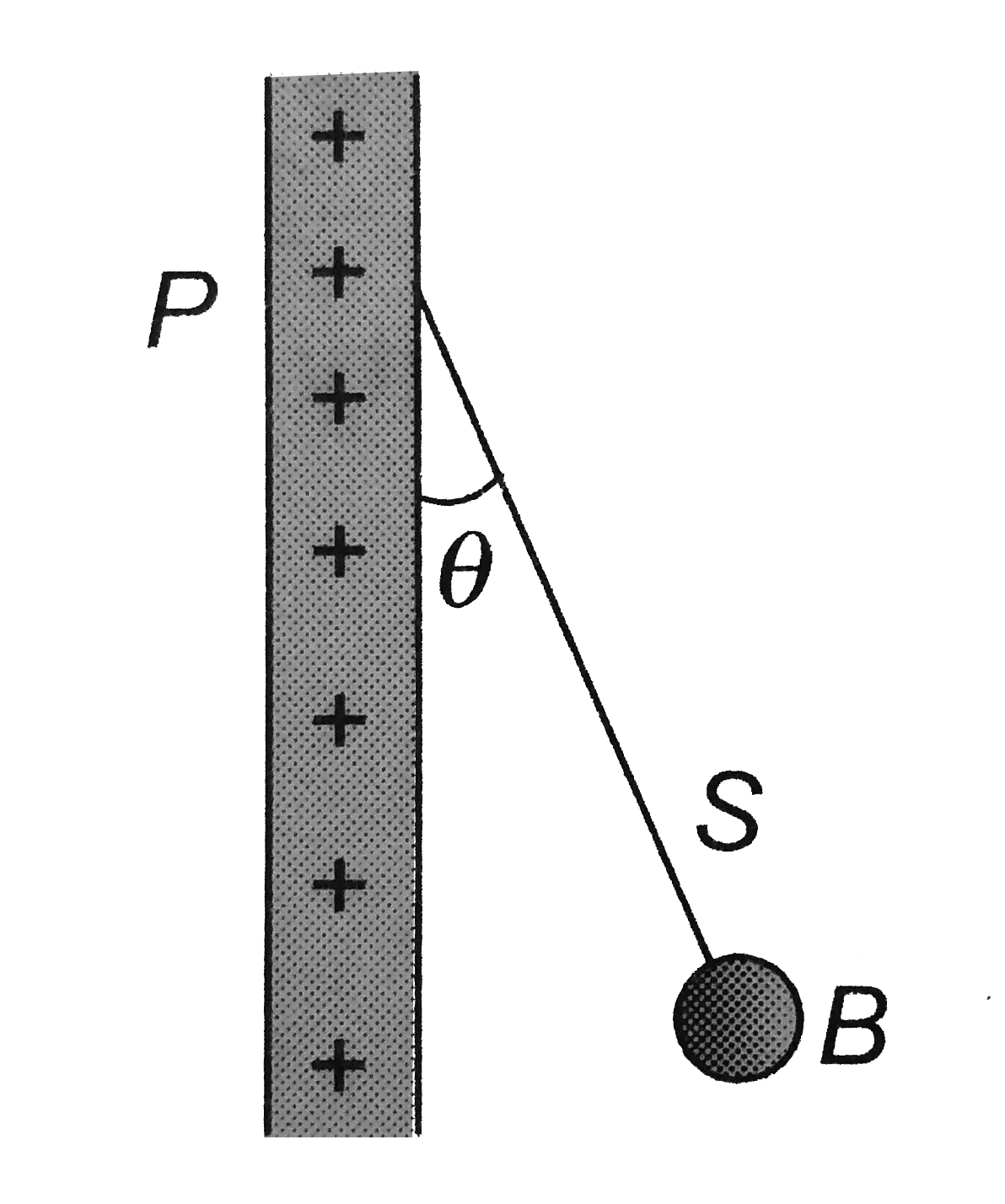
View SolutionA circular metal plate of radius 10 cm is given a charge of 20μC on its surface. The charge density of the plate is
View SolutionA sphere has surface charge density σ. It is surrounded by a spherical shell. The surface charge density on the spherical shell is
View Solution
