A small object of mass of 100 g moves in a circular path. At a given instant velocity of the object is 10ˆim/s and acceleration is (20ˆi+10ˆj)m/s2. At this instant of time, rate of change of kinetic energy (in kg m2s−3) of the object is
The correct Answer is:20
To find the rate of change of kinetic energy of the object, we can follow these steps:
Step 1: Understand the Kinetic Energy Formula
The kinetic energy (KE) of an object is given by the formula:
KE=12mv2
where m is the mass of the object and v is its velocity.
Step 2: Differentiate Kinetic Energy with Respect to Time
To find the rate of change of kinetic energy with respect to time, we differentiate the kinetic energy formula:
d(KE)dt=ddt(12mv2)
Using the chain rule, we get:
d(KE)dt=12m⋅2v⋅dvdt=mvdvdt
Step 3: Identify Given Values
From the problem:
- Mass m=100g=0.1kg (convert grams to kilograms)
- Velocity v=10m/s
- Acceleration a=(20^i+10^j)m/s2
Step 4: Calculate dvdt
The acceleration a is the rate of change of velocity with respect to time:
dvdt=a=(20^i+10^j)m/s2
Step 5: Calculate the Dot Product
To find v⋅dvdt, we need to compute the dot product:
- Velocity vector v=10^i
- Acceleration vector a=(20^i+10^j)
Calculating the dot product:
v⋅a=(10^i)⋅(20^i+10^j)=10⋅20+0=200
Step 6: Substitute Values into the Rate of Change of Kinetic Energy
Now substitute the values into the formula for the rate of change of kinetic energy:
d(KE)dt=mvdvdt=0.1kg⋅10m/s⋅200m/s2
d(KE)dt=0.1⋅10⋅200=200kg m2/s3
Final Answer
The rate of change of kinetic energy of the object is:
d(KE)dt=200kg m2/s3
---
The kinetic energy (KE) of an object is given by the formula:
KE=12mv2
where m is the mass of the object and v is its velocity.
To find the rate of change of kinetic energy with respect to time, we differentiate the kinetic energy formula:
d(KE)dt=ddt(12mv2)
Using the chain rule, we get:
d(KE)dt=12m⋅2v⋅dvdt=mvdvdt
From the problem:
- Mass m=100g=0.1kg (convert grams to kilograms)
- Velocity v=10m/s
- Acceleration a=(20^i+10^j)m/s2
The acceleration a is the rate of change of velocity with respect to time:
dvdt=a=(20^i+10^j)m/s2
To find v⋅dvdt, we need to compute the dot product:
- Velocity vector v=10^i
- Acceleration vector a=(20^i+10^j)
v⋅a=(10^i)⋅(20^i+10^j)=10⋅20+0=200
Now substitute the values into the formula for the rate of change of kinetic energy:
d(KE)dt=mvdvdt=0.1kg⋅10m/s⋅200m/s2
d(KE)dt=0.1⋅10⋅200=200kg m2/s3
The rate of change of kinetic energy of the object is:
d(KE)dt=200kg m2/s3
Topper's Solved these Questions
Similar Questions
An object of mass 1 kg is moving with a velocity 10 m/s. Find the kinetic energy of the object
View SolutionA particle is moving in an isolated x−y plane. At an instant, the particle has velocity (4ˆi+4ˆj)m/s and acceleration (3ˆi+5ˆj)m/s2. At that instant what will be the radius of curvature of its path ?
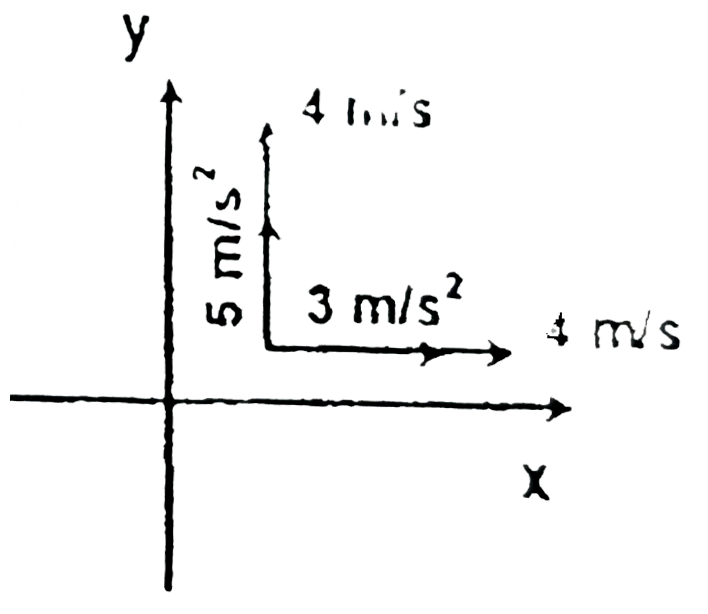
View Solution
Knowledge Check
A small object of mass of 100 g moves in a circular path . At a given instant velocity of the object is 10ˆims−1 and acceleration is (20ˆi+10ˆj)ms−2. At this instant of time. the rate of change of kinetic energy of the object is
A200kg m2s−2B300kg m2s−2C10000kg m2s−2D20kg m2s−2A particle of mass 2kg starts moving in a straight line with an initial velocity of 2m/s at a constant acceleration of 2m/s2. Then rate of change of kinetic energy.
Ais four times the velocity at any momentBis two times the displacement at any momentCis four times the rate of charge of velocity at any momentDis constant throughoutAn object of 1kg mass has a momentum of 10 kg m / sec then the kinetic energy of the object will be
A100JB50JC1000JD200J
A particle is moving in such a way that at one instant velocity vector of the particle is 3ˆi+4ˆjm/s and acceleration vector is −25ˆi−25ˆjm/s? The radius of curvature of the trajectory of the particle at that instant is
View SolutionA car of mass m moves in a horizontal circular path of radius r metre. At an instant its speed is Vm/s and is increasing at a rate of am/sec2.then the acceleration of the car is
View SolutionAn object of 10 kg is moving with a speed of 2 m/s. The kinetic energy of the object is:
View SolutionAn object of 10 kg is moving with a speed of 2 m/s. The kinetic energy of the object is:
View SolutionA particle is moving on a circular path of 10 m radius. At any instant of time, its speed is 5ms−1 and the speed is increasing at a rate of 2ms−2. At this instant, the magnitude of the net acceleration will be
View Solution
