Two spherical conductors of radii 4 m and 5 m are charged to the same potential. If $σ_{1} and σ_{2}$ be the respective value of the surface density of charge on the two conductors, then the ratio $\frac{σ_{1}}{σ_{2}}$ is

A

$\frac{25}{16}$

B

$\frac{16}{25}$

C

$\frac{5}{4}$

D

$\frac{4}{5}$

Video Solution

Text Solution

Generated By DoubtnutGPT

The correct Answer is:C

To solve the problem, we need to find the ratio of the surface charge densities ( $σ_{1}$ and $σ_{2}$ ) of two spherical conductors that are charged to the same potential. The radii of the conductors are given as $R_{1} = 4 m$ and $R_{2} = 5 m$ .
1. Understanding the Potential of Spherical Conductors:
The potential $V$ of a spherical conductor is given by the formula:
$V = \frac{K Q}{R}$
where $K$ is the electrostatic constant, $Q$ is the charge, and $R$ is the radius of the sphere.
2. Setting Up the Equation for Both Conductors:
Since both conductors are charged to the same potential $V$ , we can write:
$V_{1} = \frac{K Q_{1}}{R_{1}} and V_{2} = \frac{K Q_{2}}{R_{2}}$
Since $V_{1} = V_{2}$ , we have:
$\frac{K Q_{1}}{R_{1}} = \frac{K Q_{2}}{R_{2}}$
3. Simplifying the Equation:
The constant $K$ cancels out, leading to:
$\frac{Q_{1}}{R_{1}} = \frac{Q_{2}}{R_{2}}$
Rearranging gives us:
$\frac{Q_{1}}{Q_{2}} = \frac{R_{1}}{R_{2}}$
4. Calculating Surface Charge Densities:
The surface charge density $σ$ is defined as:
$σ = \frac{Q}{A}$
For a spherical conductor, the surface area $A$ is $4 π R^{2}$ . Therefore, we can express $σ_{1}$ and $σ_{2}$ as:
$σ_{1} = \frac{Q_{1}}{4 π R_{1}^{2}} and σ_{2} = \frac{Q_{2}}{4 π R_{2}^{2}}$
5. Finding the Ratio of Surface Charge Densities:
The ratio $\frac{σ_{1}}{σ_{2}}$ can be expressed as:
$\frac{σ_{1}}{σ_{2}} = \frac{Q_{1}}{Q_{2}} \cdot \frac{R_{2}^{2}}{R_{1}^{2}}$
Substituting $\frac{Q_{1}}{Q_{2}} = \frac{R_{1}}{R_{2}}$ into the equation gives:
$\frac{σ_{1}}{σ_{2}} = \frac{R_{1}}{R_{2}} \cdot \frac{R_{2}^{2}}{R_{1}^{2}}$
This simplifies to:
$\frac{σ_{1}}{σ_{2}} = \frac{R_{2}}{R_{1}}$
6. Substituting the Values:
Now, substituting the values of the radii:
$R_{1} = 4 m and R_{2} = 5 m$
We find:
$\frac{σ_{1}}{σ_{2}} = \frac{5}{4}$
Final Answer:
Thus, the ratio of the surface charge densities is:
$\frac{σ_{1}}{σ_{2}} = \frac{5}{4}$

Updated on:7/8/2024

|

Class 12 PHYSICS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

Two spherical conductors of radii $4 c m and 5 c m$ are charged to the same potential. If $σ_{1} and σ_{2}$ be respective value of surface density of charge on both the conductors, then the ratio of $σ_{1} / σ_{2}$ will be
A $\frac{16}{25}$
B $\frac{15}{10}$
C $\frac{4}{5}$
D $\frac{5}{4}$
Two spheres of radii 2 cm and 3 cm are charged to the same potential. If $σ$ and $σ_{2}$ be respectively the values of surface charge density on the conductors, then the ratio $\frac{σ_{1}}{σ_{2}}$ will be
A $\frac{4}{9}$
B $\frac{2}{3}$
C $\frac{3}{2}$
D $\frac{9}{4}$
The V-I graph is given for two conductors of same area and length. If $σ_{1} and σ_{2}$ are the cnductivities of the conductors 1 and 2 respectively, $\frac{σ_{1}}{σ_{2}} =$

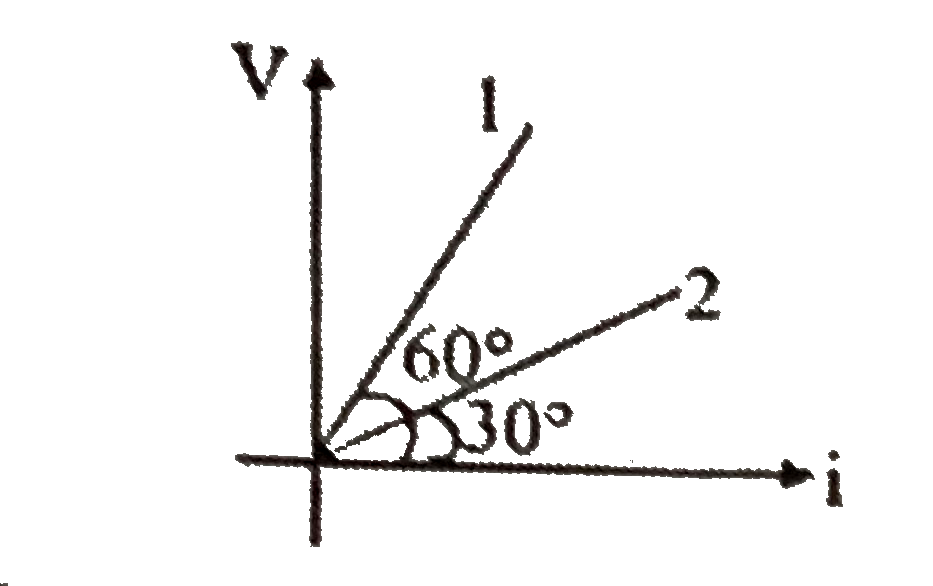A $2 : 1$
B $3 : 1$
C $1 : \sqrt{2}$
D $1 : 3$

NTA MOCK TESTS-NTA JEE MOCK TEST 79-PHYSICS

Home
Ask Doubt
Profile