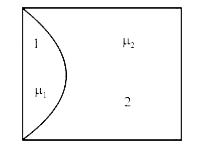
One plano -convex and one plano-concave lens of same radius of curvature R but of different materials are joined side by side as shown in the figure. If the refractive index of the meterial of 1 is μ1 and that of 2 is μ2, then the focal length of the combination is:
R2−(μ1−μ2)
R2(μ1−μ2)
2Rμ1−μ2
Rμ1−μ2
The correct Answer is:D
Step by step video, text & image solution for One plano -convex and one plano-concave lens of same radius of curvature R but of different materials are joined side by side as shown in the figure. If the refractive index of the meterial of 1 is mu_(1) and that of 2 is mu_(2), then the focal length of the combination is: by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Find the radius of curvature of the convex surface of a plano-convex lens, whose focal length is 0.3 m and the refractive index of the material of the lens is 1.5.
View SolutionFind the radius of curvature of the convex surface of a plano-convex lens, whose focal length is 0.3 m and the refractive index of the material of the lens is 1.5.
View Solution
Knowledge Check
If in a plano-convex lens, the radius curvature of the convex surface is 10 cm and the focal length of the lens is 30 cm, then the refractive index of the material of lens will be
A1.5B1.66C1.33D3If in a plano-convex lens, the radius of curvature of the convex surface is 10 cm and the focal length of the lens is 30 cm , then the refractive index of the material of lens will be
A1.5B1.66C1.33D3The radius of curvature of the curved surface of a plano-convex lens is 20cm. If the refractive index of the material of the lens be 1.5, it will
Aact as a convex lens only for the object that lie on its curved side.Bact as a concave lens for the objects that lie on its curved side.Cact as a convex lens irrespective of the side on which the object lies.Dact as a concave lens irrespective of side on which the object lies.
Find the radius of curvature of the convex surface of a plan-convex lens, whose focal length is 0.3 m and the refractive index of the material of the lens is 1.5.
View SolutionIf in a plano-convex lens, the radius curvature of the convex surface is 10 cm and the focal length of the lens is 20 cm , then the refractive index of the material of lens will be
View SolutionFor a plano convex lens, the radius of curvature of convex surface is 10 cm and the focal length is 30 cm. The refractive index of the material of the lens is
View SolutionThe radius of curvature of the convex face of a plano convex lens is 12cm and the refractive index of the material of the lends 1.5. Then, the focal length of the lens is
View SolutionThe radius of curvature of the curved surface of a plano-convex lens is 20cm. If the refractive index of the material of the lens be 1.5, it will
View Solution
