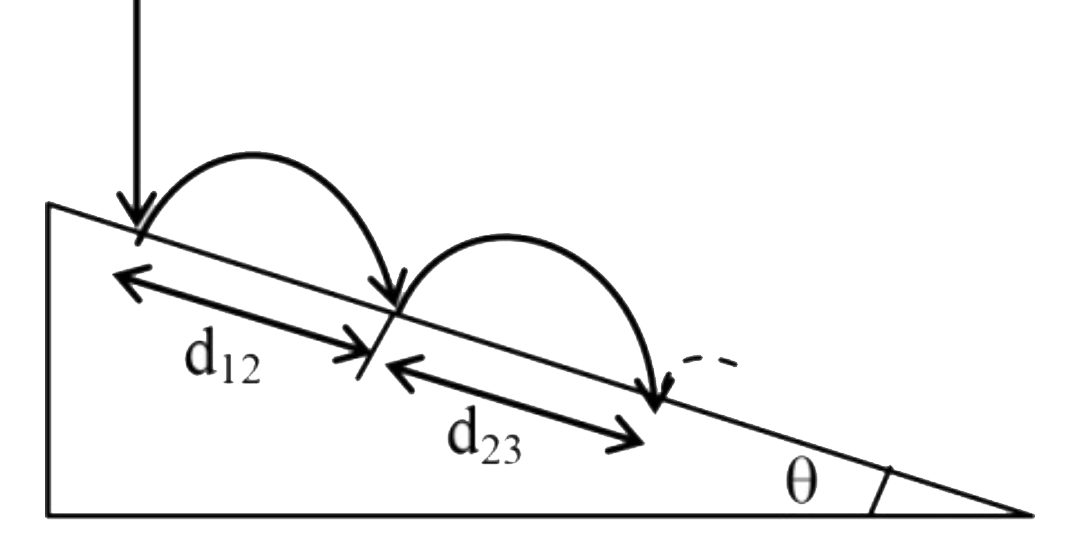
An elastic ball is dropped on a long inclined plane. If bounces, hits the plane again, bounces and so on. Let us Label the distance between the point of the first and second hit d12 and the distance between the points of second and the third hit is d23. find the ratio of d12/d23.
21
12
41
14
The correct Answer is:B
Step by step video, text & image solution for An elastic ball is dropped on a long inclined plane. If bounces, hits the plane again, bounces and so on. Let us Label the distance between the point of the first and second hit d_(12) and the distance between the points of second and the third hit is d_(23). find the ratio of d_(12)//d_(23). by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Find the distance between points C(−3a,a)andD(a,−2a)
View Solution
A ball is released in air above an incline plane inclined at an angle α to the horizontal. After falling vertically through a distance h it hits the incline and rebounds. The ball flies in air and then again makes an impact with the incline. This way the ball rebounds multiple times. Assume that collisions are elastic, i.e., the ball rebound without any loss in speed and in accordance to the law of reflection.
(a) Distance between the points on the incline where the ball makes first and second impact is l1 and distance between points where the ball makes second and third impact is l2. Which is large l1 or l2?
(b) Calculate the distance between the points on the incline where the ball makes second and fifth impact.
View Solution
Knowledge Check
The sides of a triangle ABC are as shown in the given figure. Let D be any internal point of this triangle and let e,f and g denote the distance between the point D and the sides of the triangle. The sum (5e+12f+13g) is equal to
 A120B90C60D30
A120B90C60D30
If the distance between the points P(acos48∘,0)andQ(0,acos12∘) is d, then d2−a2=
View SolutionIf the distance between the points (acos480,0) and (0,acos12∘) is d, then d2−a2=
View SolutionFind the distance between the point P(6,5,9)and the plane determined by the points A(3,1,2), B(5,2,4)and C(1,1,6).
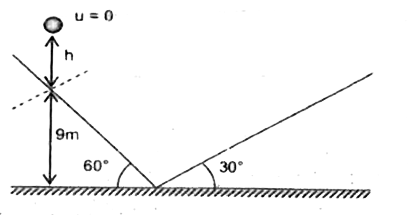
View SolutionA ball is dropped from a height h on a inclined plane, ball collides elastically with the first plane. Find the value of 'h' (in meter) so that it strikes perpendicular on the second inclined plane.
View SolutionIn a class room 4 friends are seated at the point A,B,C,D as shown in figure.
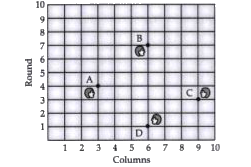
Find the distance between A and D.
View SolutionThe sides of a triangle ABC are as shown in the given figure. Let D be any internal point of this triangle and let e, f, and g denote the distance between the point D and the sides of the triangle. The sum (5e+12f+13g) is equal to
View SolutionIn a class room 4 friends are seated at the point A,B,C,D as shown in figure.
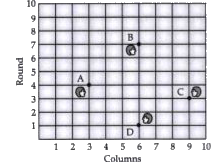
Find the distance between B and C.
View Solution
