In the YDSE arrangement shown here, the intensity on the screen due to slit -2 is four times that of slit -1. If resultant intensity at the position of central maxima O is I, the resultant intensity at point P, where the phase difference between two waves coming from two slits is cos−1(14) is
I3
2I3
I4
I2
The correct Answer is:B
To solve the problem, we need to find the resultant intensity at point P in a Young's Double Slit Experiment (YDSE) setup, given that the intensity from slit 2 is four times that from slit 1.
1. Define Intensities from Each Slit:
Let the intensity from slit 1 be I1=I0 and the intensity from slit 2 be I2=4I0.
2. Resultant Intensity at Central Maxima (O):
The resultant intensity at the central maxima (point O) is given as I. Using the formula for resultant intensity in YDSE:
I=I1+I2+2√I1I2cosϕ
At the central maxima, the phase difference ϕ=0 (since the path difference is zero), so cosϕ=1:
I=I0+4I0+2√I0⋅4I0⋅1
I=5I0+2⋅2I0=5I0+4I0=9I0
3. Express I0 in Terms of I:
From the above, we have:
I=9I0⟹I0=I9
4. Phase Difference at Point P:
The phase difference at point P is given as ϕ=cos−1(14).
5. Resultant Intensity at Point P:
We will use the same formula for resultant intensity at point P:
IP=I1+I2+2√I1I2cosϕ
Substituting I1=I0, I2=4I0, and cosϕ=14:
IP=I0+4I0+2√I0⋅4I0⋅14
IP=I0+4I0+2⋅2I0⋅14
IP=5I0+I0=6I0
6. Substituting I0 in Terms of I:
Now substituting I0=I9:
IP=6⋅I9=23I
Final Result:
The resultant intensity at point P is:
23I
Let the intensity from slit 1 be I1=I0 and the intensity from slit 2 be I2=4I0.
The resultant intensity at the central maxima (point O) is given as I. Using the formula for resultant intensity in YDSE:
I=I1+I2+2√I1I2cosϕ
At the central maxima, the phase difference ϕ=0 (since the path difference is zero), so cosϕ=1:
I=I0+4I0+2√I0⋅4I0⋅1
I=5I0+2⋅2I0=5I0+4I0=9I0
From the above, we have:
I=9I0⟹I0=I9
The phase difference at point P is given as ϕ=cos−1(14).
We will use the same formula for resultant intensity at point P:
IP=I1+I2+2√I1I2cosϕ
Substituting I1=I0, I2=4I0, and cosϕ=14:
IP=I0+4I0+2√I0⋅4I0⋅14
IP=I0+4I0+2⋅2I0⋅14
IP=5I0+I0=6I0
Now substituting I0=I9:
IP=6⋅I9=23I
The resultant intensity at point P is:
23I
Topper's Solved these Questions
Similar Questions
In a standard YDSE set up,the intensity at a point where phase difference between the light from the slits is π3 is I0 .The intensity of central maximum will be ?
View SolutionS1 and S2 are two equally intense coherent point second sources vibrating in phase. The resultant intensity at P1 is 80SI units then resultant intensity at P2 in SI units will be
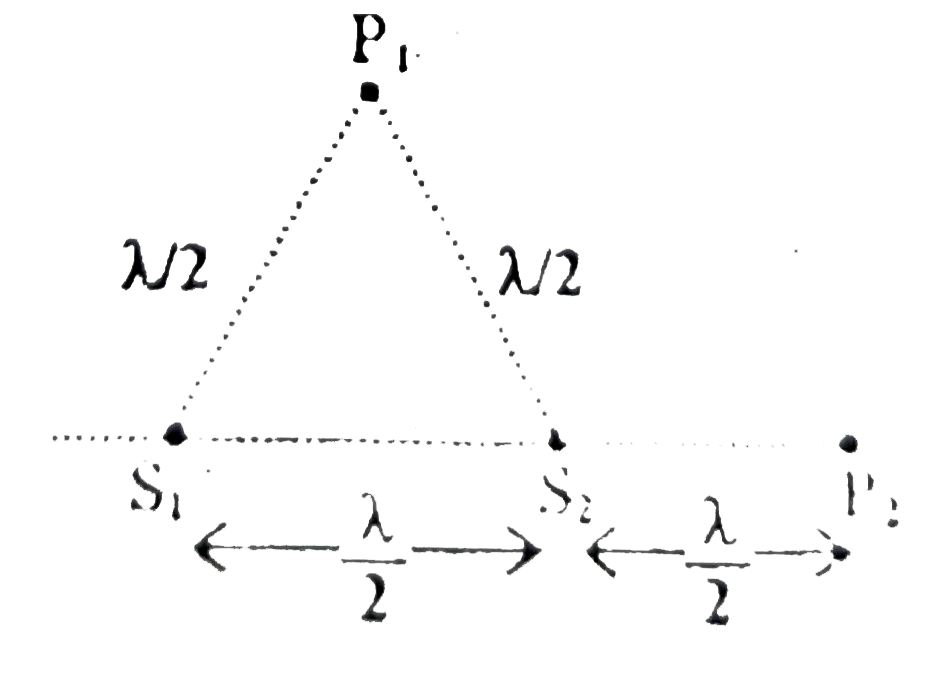
View Solution
Knowledge Check
Two waves having intensity Iand9I produce interference . If the resultant intensity at a point is 7I, what is the phase difference between the two waves ?
A0∘B60∘C90∘D120∘Two coherent waves of intensities I and 4I interfere at a point. If the resultant intensity is 3I, then the phase difference between te two waves at the point is
AzeroB60∘C120∘D90∘In Young's experiment intensity at a point on the scrren is 75% of the maximum value. Minimum phase difference between the waves arriving at this point from the two slits will be
A30∘B45∘C60∘D135∘
Ratio of intensities between a point A and that of central fringe is 0.853. If we consider slits are of equal width then path difference between two waves at point A will be :
View SolutionIn a Young's double slit experiment the amplitudes of the two waves incident on the two slits are A and 2A. If I0 is the maximum intensity, then the intensity at a spot on the screen where the phase difference between the two interfering waves is ϕ .
View SolutionIt is found that what waves of same intensity from two coherent sources superpose at a certain point, then the resultant intensity is equal to the intensity of one wave only. This means that the phase difference between the two waves at that point is
View SolutionIn Young's double slit experiment, the maximum intensity is I0. What is the intensity at a point on the screen where the path difference between the interfering waves is λ4 ?
View SolutionIn Young's double slit experiment the ratio of intensities at the position of maxima and minima is 9/1. the ratio of amplitudes of light waves is
View Solution
