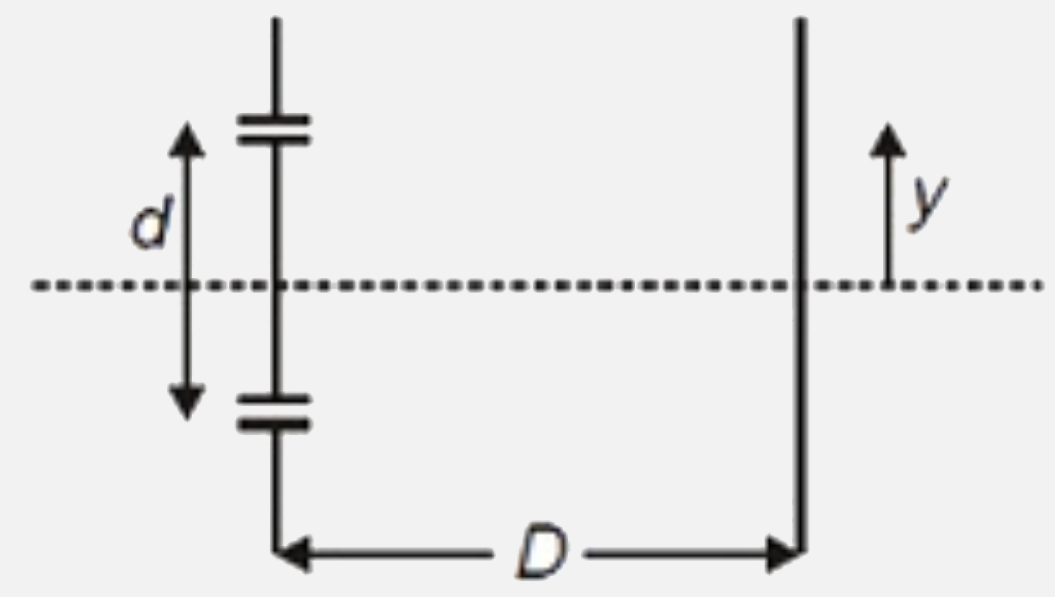
In YDSE a parallel beam of incident light consists of two wavelengths $λ_{1} = 4000 Å and λ_{2} = 5600 Å$ . The minimum distance y on the screen, measured from the central axis, where the bright fringe due to two wavelengths coincide is $\frac{n λ_{1} D}{d}$ . Find n.

Video Solution

Text Solution

Verified by Experts

The correct Answer is:7

|

Answer

Step by step video & image solution for In YDSE a parallel beam of incident light consists of two wavelengths lambda_(1)=4000Å and lambda_(2)=5600Å. The minimum distance y on the screen, measured from the central axis, where the bright fringe due to two wavelengths coincide is (nlambda_(1)D)/(d). Find n. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 PHYSICS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One or More
Bichromatic light of wavelengths $λ_{1} = 5000 Å and λ_{2} = 7000 Å$ are used in YDSE. Then,
A14th order maxima of $λ_{1}$ will coincide with 10th order maxima of $λ_{2}$
B21st order maxima of $λ_{2}$ will coincide with 15th order maxima of lambda_1
C11th order minima of $λ_{1} w i l l c o \in c w i t h 8 t h or d e r min i m a o f$ lambda_2
D3rd order minima of $λ_{1}$ will coincide with 4th order minima of $λ_{2}$
Question 2 - Select One
The ratio of resolving power of an optical microscope for two wavelength $λ_{1} = 4000 Å$ and $λ_{2} = 6000 Å$ is:
A $9 : 4$
B $3 : 2$
C $16 : 81$
D $8 : 27$
Question 3 - Select One
The ratio of resolving power of an optical microscope for two wavelength $λ_{1} = 4000 Å$ and $λ_{2} = 6000 Å$ is:
A $9 : 4$
B $3 : 2$
C $16 : 81$
D $8 : 27$

NTA MOCK TESTS-NTA JEE MOCK TEST 102-PHYSICS

Home
Ask Doubt
Profile