The overall rate d[P]dt, for the reaction 2AK⇐⇒B,B+Ckf−−→P is given by
Kkf[A]2[C]
K[A][B]
kf[B][C]
Kkf[A]2[B][C]
The correct Answer is:A
To solve the problem, we need to derive the overall rate of the reaction given by:
2AK⇌B
B+Ckf→P
1. Identify the Reaction Components:
- The first part of the reaction is an equilibrium reaction where 2 moles of A produce 1 mole of B.
- The second part of the reaction involves B and C reacting to form product P.
2. Write the Equilibrium Constant Expression:
- For the equilibrium reaction 2A⇌B, the equilibrium constant K is given by:
K=(B)(A)2
3. Express Concentration of B:
- Rearranging the equilibrium constant expression gives us:
(B)=K⋅(A)2
4. Write the Rate of Formation of P:
- The rate of the reaction forming P from B and C can be expressed using the rate constant kf:
Rate=kf(B)(C)
5. Substitute (B) into the Rate Expression:
- Now substitute the expression for (B) from step 3 into the rate expression:
Rate=kf(K⋅(A)2)(C)
6. Final Expression for Overall Rate:
- Therefore, the overall rate of formation of P can be expressed as:
d(P)dt=kfK(A)2(C)
Conclusion:
The overall rate of the reaction is given by:
d(P)dt=kfK(A)2(C)
B+Ckf→P
- The first part of the reaction is an equilibrium reaction where 2 moles of A produce 1 mole of B.
- The second part of the reaction involves B and C reacting to form product P.
- For the equilibrium reaction 2A⇌B, the equilibrium constant K is given by:
K=(B)(A)2
- Rearranging the equilibrium constant expression gives us:
(B)=K⋅(A)2
- The rate of the reaction forming P from B and C can be expressed using the rate constant kf:
Rate=kf(B)(C)
- Now substitute the expression for (B) from step 3 into the rate expression:
Rate=kf(K⋅(A)2)(C)
- Therefore, the overall rate of formation of P can be expressed as:
d(P)dt=kfK(A)2(C)
The overall rate of the reaction is given by:
d(P)dt=kfK(A)2(C)
Topper's Solved these Questions
Similar Questions
Knowledge Check
Conisder the following reactions:
I. A+Bk1⇐⇒k−1C
II. C+Bk2−−→D
Then k1[A][B]−k−1[C]−k2[C][B] is equal toA−d[A]dtB−d[B]dtCd[C]dtDd[D]dtConsider the following reactions,
A+Bk1⇐⇒k−1C,C+Bk2−−→D
The rate in terms of −d[B]dt will beAk1[A][B]−k−1[C]Bk1[A][B]−k1[C]−k2[C][B]Ck1[A][B]−k2[C][B]Dk1[A][B]−k−1[C]+k2[C][B]The relation between KPandKC for the reaction A(g)+B(g)⇔C(g)+2D(g) is -
AKP=KC[RT]−1BKP.KC−1=RTCKCKP−1=RTDKP=KC[RT]3
Mechanism of the reaction is:
A2k1⇐⇒2A
A+Bk2−−→C
A2+Ck−−→D+A
What is (a) −d[A2]dt, (b) −d[A]dt, (c ) d[C]dt, (d) d[D]dt ?
View SolutionMechanism of the reaction is:
Ak2⇐⇒k1B ...(i)
B+Ak3⇐⇒C ...(ii)
¯¯¯¯¯¯¯¯¯¯¯¯¯¯2A→C––––––––– ...(iii)
What is (a) −d[A]dt, (b) d[B]dt , (c ) d[C]dt
View SolutionConisder the following proposed mechanism
Ak2⇐⇒k1B , B+Ck3−−→D
For the overall reaction A+C→D, assuming B to be an intermediate described by the steady state approximation, write the rate expresison for [A].
View SolutionConsider the reaction mechanism:
A2keq⇐⇒2A(fast) (where A is the intermediate.)
A+B−−→k1P(slow)
The rate law for the reaction is
View SolutionAn enzyme [E] is combined with the substrate [S] as follows:
E+SK1⇐⇒K−1ES
ESK2−−→P+E
The overall reaction rate is given by:
Rate =Vmax[S]Km+[S] and the rate of reaction varies with substrate concentration as:
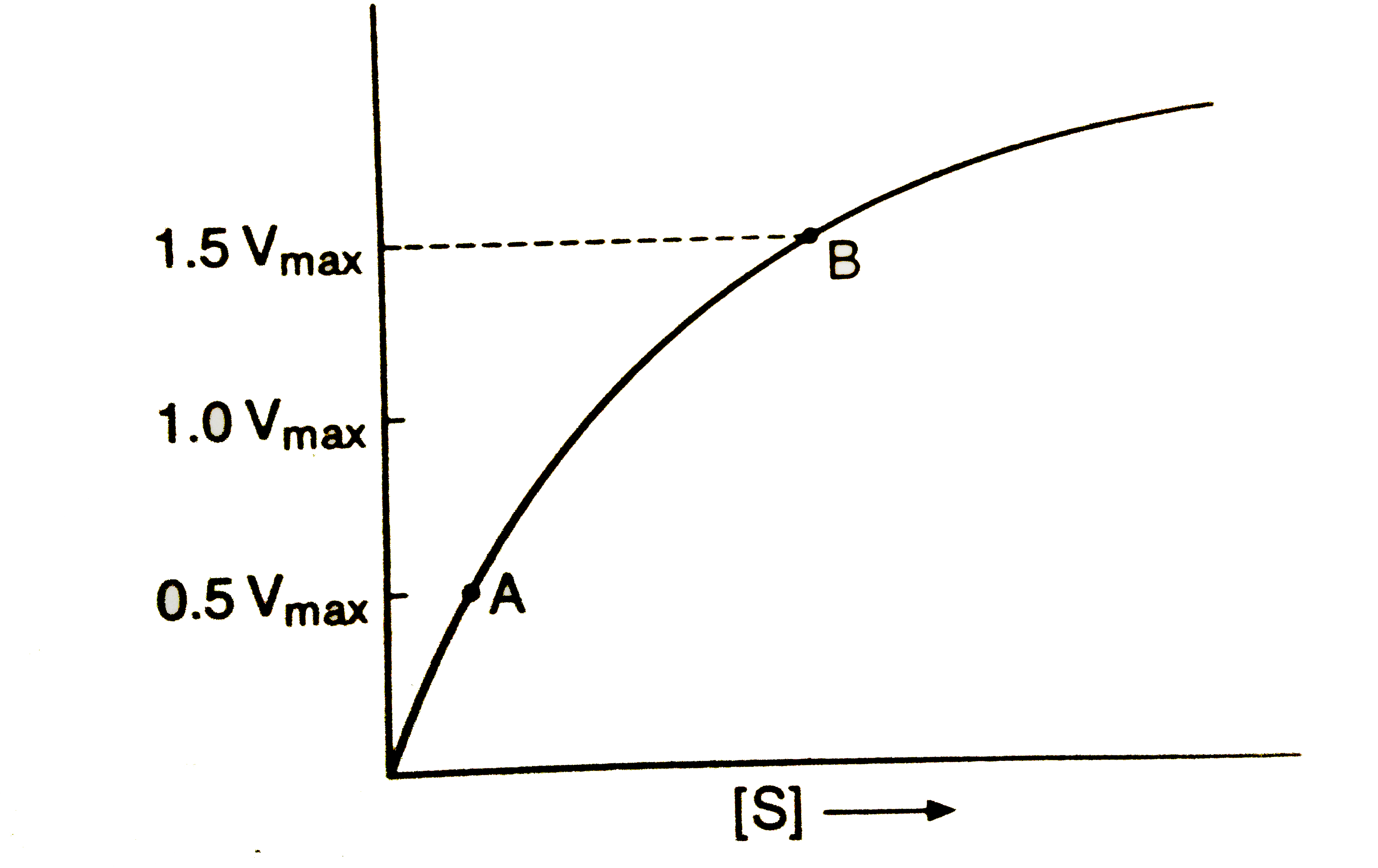
The order of reaction at point A is :
View Solution
