Let a fully charged lead storage battery contains 1.5 L 5 M H2SO4. What will be the concentration of H2SO4 in the battery after 2.5 ampere current is drawn from the battery for 6 hour?
4.626 M
0.1865 M
0.373 M
9.627 M
The correct Answer is:A
To find the concentration of H₂SO₄ in the battery after a current is drawn, we can follow these steps:
Step 1: Calculate the Initial Moles of H₂SO₄
Given:
- Volume of H₂SO₄ solution = 1.5 L
- Molarity of H₂SO₄ = 5 M
Using the formula for moles:
\(
\text{Moles of } H₂SO₄ = \text{Molarity} \times \text{Volume} = 5 \, \text{mol/L} \times 1.5 \, \text{L} = 7.5 \, \text{moles}
\)
Step 2: Calculate the Total Charge Passed
Given:
- Current (I) = 2.5 A
- Time (t) = 6 hours = 6 × 3600 seconds = 21600 seconds
Using the formula for charge:
\(
Q = I \times t = 2.5 \, \text{A} \times 21600 \, \text{s} = 54000 \, \text{C}
\)
Step 3: Calculate the Moles of Electrons Transferred
Using Faraday's constant (F = 96500 C/mol):
\(
\text{Moles of electrons} = \frac{Q}{F} = \frac{54000 \, \text{C}}{96500 \, \text{C/mol}} \approx 0.56 \, \text{moles}
\)
Step 4: Relate Moles of H₂SO₄ to Moles of Electrons
From the cell reaction, we see that 1 mole of H₂SO₄ corresponds to 2 moles of electrons. Therefore, the moles of H₂SO₄ consumed can be calculated as:
\(
\text{Moles of } H₂SO₄ \text{ consumed} = \frac{0.56}{2} = 0.28 \, \text{moles}
\)
Step 5: Calculate Remaining Moles of H₂SO₄
Subtract the moles of H₂SO₄ consumed from the initial moles:
\(
\text{Remaining moles of } H₂SO₄ = 7.5 \, \text{moles} - 0.28 \, \text{moles} = 7.22 \, \text{moles}
\)
Step 6: Calculate the New Concentration of H₂SO₄
Using the remaining moles and the original volume:
\(
\text{New concentration} = \frac{\text{Remaining moles}}{\text{Volume}} = \frac{7.22 \, \text{moles}}{1.5 \, \text{L}} \approx 4.81 \, \text{M}
\)
Final Answer:
The concentration of H₂SO₄ in the battery after the current is drawn will be approximately 4.81 M.
---
Given:
- Volume of H₂SO₄ solution = 1.5 L
- Molarity of H₂SO₄ = 5 M
\(
\text{Moles of } H₂SO₄ = \text{Molarity} \times \text{Volume} = 5 \, \text{mol/L} \times 1.5 \, \text{L} = 7.5 \, \text{moles}
\)
Given:
- Current (I) = 2.5 A
- Time (t) = 6 hours = 6 × 3600 seconds = 21600 seconds
\(
Q = I \times t = 2.5 \, \text{A} \times 21600 \, \text{s} = 54000 \, \text{C}
\)
Using Faraday's constant (F = 96500 C/mol):
\(
\text{Moles of electrons} = \frac{Q}{F} = \frac{54000 \, \text{C}}{96500 \, \text{C/mol}} \approx 0.56 \, \text{moles}
\)
From the cell reaction, we see that 1 mole of H₂SO₄ corresponds to 2 moles of electrons. Therefore, the moles of H₂SO₄ consumed can be calculated as:
\(
\text{Moles of } H₂SO₄ \text{ consumed} = \frac{0.56}{2} = 0.28 \, \text{moles}
\)
Subtract the moles of H₂SO₄ consumed from the initial moles:
\(
\text{Remaining moles of } H₂SO₄ = 7.5 \, \text{moles} - 0.28 \, \text{moles} = 7.22 \, \text{moles}
\)
Using the remaining moles and the original volume:
\(
\text{New concentration} = \frac{\text{Remaining moles}}{\text{Volume}} = \frac{7.22 \, \text{moles}}{1.5 \, \text{L}} \approx 4.81 \, \text{M}
\)
The concentration of H₂SO₄ in the battery after the current is drawn will be approximately 4.81 M.
Topper's Solved these Questions
Similar Questions
Suppose a fully charged battery containes 1.50 litre of 5.0MH2SO4. What will be the concentration of H2SO4 left in battery after 2.50 ampere current is drawn from the battery for 6.0 hour? Assume volume of solution ramains constant.
View SolutionThe storage battery of a car has an emf of 12 V. If the inernal resistance of the battery of 0.4Ω, What is the maximum current that can be drawn from the battery ?
View Solution
Knowledge Check
Excess of PCl5 reacts with concentrated H2SO4 giving :
AChlorosulphonic acidBSulphurous acidCSulphuryl chlorideDThionlyl chlorideWhen lead storage battery discharges , specific gravity of H2SO4 decreases to
AzeroB1.17C1.28D1.2155 moles of H2SO4 contain
A5 eq. of HB5 moles of SC20 eq. of OD10 eq. each of H, S and O
The storage battery of a car has an emf of 12 V. If the internal resistance of the battery is 0.4Ω, what is the maximum current that can be drawn from the battery ?
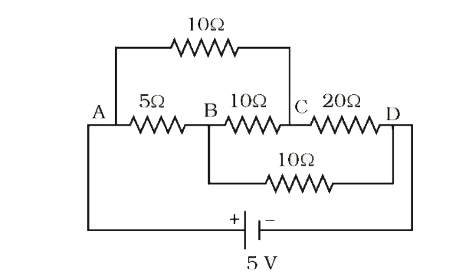
View SolutionCalculate the value of the current drawn from a 5V battery in the circuit as shown
View SolutionA storage battery contains a solution of H2SO438% by weight. At this concentration, the Vant't Hoff factor is 2.50. At what temperature will the battery contents freeze? (Kf=1.86∘mol−1kg)
View SolutionBattery acid is 4.27 M H2SO4 (aq) and has density of 1.25mL−1 . What is the molality of H2SO4 in the solution ?
View SolutionFully charges lead storage battery contains 1.5 L of 5MH2SO4. If 2.5 amp of currect is taken from the cell for 965 minutes, then what will be the molarity of remaining H2SO4 ? Assume that volume of battery fluid to be constant :
View Solution
