Mg(s)∣∣Mg2+(aq)∣∣∣∣Zn2+(aq)∣∣Zn(s),E∘=+3.13V
The correct plot of Ecell versus log.[Mg2+][Zn2+] will be represented as
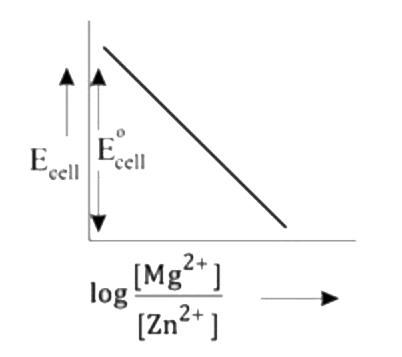
The correct Answer is:B
To solve the problem, we need to analyze the electrochemical cell given and apply the Nernst equation to plot the relationship between the cell potential (E_cell) and the logarithm of the concentration ratio of the ions involved.
1. Identify the Half-Reactions:
- At the anode (oxidation):
Mg(s)→Mg2+(aq)+2e−
- At the cathode (reduction):
Zn2+(aq)+2e−→Zn(s)
2. Write the Overall Cell Reaction:
The overall cell reaction can be combined from the half-reactions:
Mg(s)+Zn2+(aq)→Mg2+(aq)+Zn(s)
3. Apply the Nernst Equation:
The Nernst equation relates the standard cell potential (E°) to the cell potential (E) under non-standard conditions:
E=E°−RTnFlog((Mg2+)(Zn2+))
Where:
- E°=+3.13V
- R is the universal gas constant (8.314 J/(mol·K))
- T is the temperature in Kelvin (assume standard temperature, 298 K)
- n=2 (number of moles of electrons transferred)
- F is Faraday's constant (96485 C/mol)
4. Rearranging the Nernst Equation:
We can rearrange the equation in the form of y=mx+c:
E=E°−RTnFlog((Mg2+)(Zn2+))
Here, y=E, x=log((Mg2+)(Zn2+)), m=−RTnF, and c=E°.
5. Determine the Slope and Intercept:
- The slope m is negative because −RTnF<0.
- The intercept c=E° is positive since E°=+3.13V.
6. Plotting the Graph:
- Since the slope is negative, the graph of Ecell versus log((Mg2+)(Zn2+)) will be a straight line that slopes downwards from left to right.
- The y-intercept will be at +3.13V.
Conclusion:
The correct plot of Ecell versus log((Mg2+)(Zn2+)) will be a straight line with a negative slope and a positive intercept.
- At the anode (oxidation):
Mg(s)→Mg2+(aq)+2e−
- At the cathode (reduction):
Zn2+(aq)+2e−→Zn(s)
The overall cell reaction can be combined from the half-reactions:
Mg(s)+Zn2+(aq)→Mg2+(aq)+Zn(s)
The Nernst equation relates the standard cell potential (E°) to the cell potential (E) under non-standard conditions:
E=E°−RTnFlog((Mg2+)(Zn2+))
Where:
- E°=+3.13V
- R is the universal gas constant (8.314 J/(mol·K))
- T is the temperature in Kelvin (assume standard temperature, 298 K)
- n=2 (number of moles of electrons transferred)
- F is Faraday's constant (96485 C/mol)
We can rearrange the equation in the form of y=mx+c:
E=E°−RTnFlog((Mg2+)(Zn2+))
Here, y=E, x=log((Mg2+)(Zn2+)), m=−RTnF, and c=E°.
- The slope m is negative because −RTnF<0.
- The intercept c=E° is positive since E°=+3.13V.
- Since the slope is negative, the graph of Ecell versus log((Mg2+)(Zn2+)) will be a straight line that slopes downwards from left to right.
- The y-intercept will be at +3.13V.
The correct plot of Ecell versus log((Mg2+)(Zn2+)) will be a straight line with a negative slope and a positive intercept.
Topper's Solved these Questions
Similar Questions
For the galvanic cell Mg(s)∣∣Mg2+(aq)∣∣∣∣Zn2+(aq)∣∣Zn(s),the standard free energy change is (Given:E∘mg2+mg=-2.36V,E∘Zn2+Zn=-0.76V)
View SolutionFor the redox reaction :
Zn(s)+Cu2+(aq)⇔Zn2+(aq)+Cu(s)
Reaction quotient (Q)=[Zn2+(aq)][Cu2+(aq)]=0.01. What will be the value of Ecell ?
Given that OA=1.10 V.

View Solution
Knowledge Check
Mg(s)∣∣Mg2+(aq)∣∣∣∣Zn2+(aq)∣∣Zn(s),E∘=+3.13V
Eसेल और log[Mg2+][Zn2+] के मध्य आलेख का सही निरूपण है :A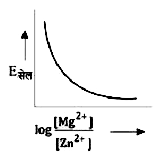 B
B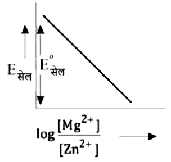 C
C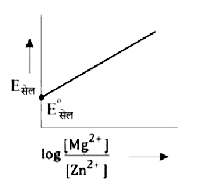 D
D
The cell reaction
Zn(s)+2Ag+(aq)→Zn2+(aq)+Ag(s)
is best represented byAAg∣∣Ag+∣∣|Zn|Zn2+BZn∣∣Zn2+∣∣∣∣Ag+∣∣AgC2Ag∣∣Ag+∣∣|Zn|Zn2+DZn∣∣Zn2+∣∣|2Ag|Ag+For the redox process
Zn(s)+Cu2+⇔Zn2++Cu(s)E∘cell=+1.10V
which graph correctly represents Ecell (Y-axis) as a function of log [Zn2+][Cu2+] (X-axis) ?A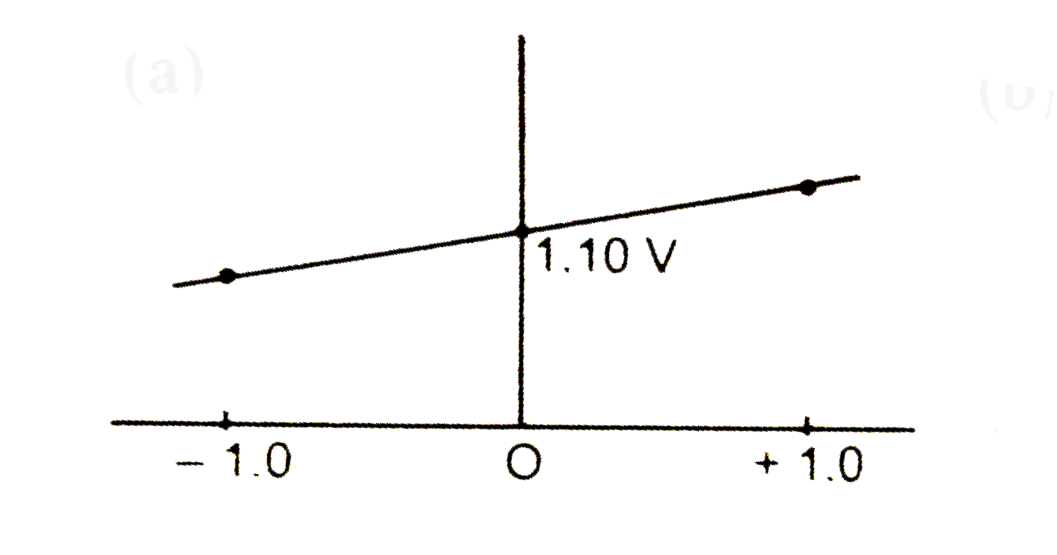 B
B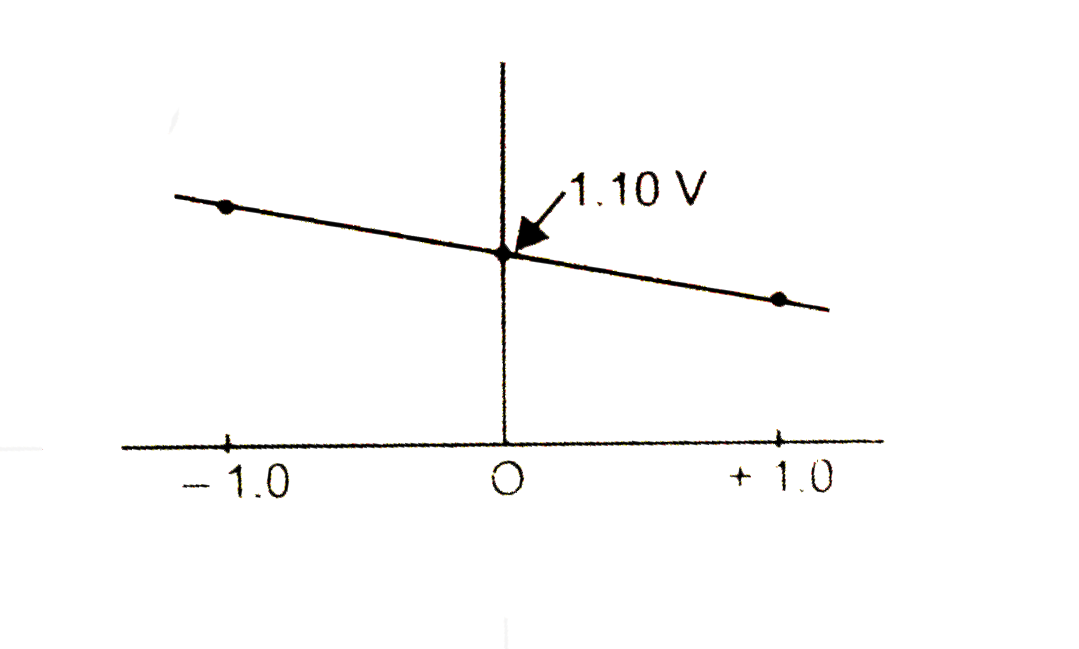 C
C D
D
For the cell reaction, Mg(s)+2Ag+(aq.)⇔Mg2+(aq.)+2Ag(s)
E∘cell is +3.17 V at 298 K. The value of Ecell,ΔG∘ and Q at Ag and Mg2+ concentration of 0.001 M and 0.02 M respectively are :
View SolutionFor the galvanic cell Zn(s)∣∣Zn2+∣∣∣∣Cd2+∣∣Cd(s),Ecell=0.30VandEocell=0.36V, then value of [Cd2+]/[Zn2+] will be:
View SolutionZn(s)+Cu2+(aq)→Zn2+(aq)+Cu(s) The cell representation for the above redox reaction is
View SolutionZn+Cu2+(aq)→Cu+Zn2+(aq).
Reaction quotient is Q=[Zn2+][Cu2+]⋅E∘cell=1.10V ltb rgt Ecell will be 1.1591 V when :

View SolutionAgaq+e−→Ag(s) E69∘)=0.80V
Mg2+(aq)+2e−→Mg(s) E∘=−2.73V
Use the equations above to calcualte the value or ΔG∘0 (in kJ/mol) for the reaction:
Mg(s)+2Ag+(aq)→Mg2+(aq)+2Ag(s)
View Solution
