The voltage of the cell consisting of Li(s)andF2(g) electrodes is 5.92 V at standard condition at 298 K. What is the voltage if the electrolyte consists of 2 M LiF.
(ln2=0.693,R=8.314 JK−1mol−1andF=96500 C mol−1)
5.90 V
5.937 V
5.88 V
4.9 V
The correct Answer is:C
To solve the problem, we need to find the voltage of the cell consisting of lithium (Li) and fluorine (F2) electrodes when the electrolyte is 2 M LiF. The standard cell potential (E°) is given as 5.92 V. We will use the Nernst equation to find the new cell potential (E).
1. Identify the Cell Reaction:
The cell reaction for the lithium and fluorine electrodes can be written as:
Li(s)+12F2(g)→Li+(aq)+F−(aq)
2. Determine the Number of Electrons (n):
In this reaction, one mole of Li loses one electron to form Li⁺. Thus, the number of electrons transferred (n) is:
n=1
3. Use the Nernst Equation:
The Nernst equation is given by:
E=E∘−RTnFlnQ
where:
- E = cell potential under non-standard conditions
- E∘ = standard cell potential (5.92 V)
- R = universal gas constant (8.314 J/(K·mol))
- T = temperature in Kelvin (298 K)
- n = number of moles of electrons (1)
- F = Faraday's constant (96500 C/mol)
- Q = reaction quotient
4. Calculate the Reaction Quotient (Q):
For the dissociation of LiF in a 2 M solution:
Q=(Li+)(F−)(F2)=(2)(2)1=4
(Assuming the pressure of F2 is 1 atm at standard conditions.)
5. Substitute Values into the Nernst Equation:
Substitute the known values into the Nernst equation:
E=5.92−(8.314)(298)(1)(96500)ln(4)
6. Calculate the Natural Logarithm:
Since ln(4)=2ln(2)=2×0.693=1.386:
E=5.92−(8.314)(298)96500×1.386
7. Calculate the Constant:
First, calculate (8.314)(298)96500:
(8.314)(298)96500≈0.0257 V
8. Final Calculation:
Now substitute this back into the equation:
E=5.92−(0.0257×1.386)≈5.92−0.0356≈5.8844 V
9. Round the Answer:
Rounding to two decimal places gives:
E≈5.88 V
Final Answer:
The voltage of the cell with 2 M LiF electrolyte is approximately 5.88 V.
The cell reaction for the lithium and fluorine electrodes can be written as:
Li(s)+12F2(g)→Li+(aq)+F−(aq)
In this reaction, one mole of Li loses one electron to form Li⁺. Thus, the number of electrons transferred (n) is:
n=1
The Nernst equation is given by:
E=E∘−RTnFlnQ
where:
- E = cell potential under non-standard conditions
- E∘ = standard cell potential (5.92 V)
- R = universal gas constant (8.314 J/(K·mol))
- T = temperature in Kelvin (298 K)
- n = number of moles of electrons (1)
- F = Faraday's constant (96500 C/mol)
- Q = reaction quotient
For the dissociation of LiF in a 2 M solution:
Q=(Li+)(F−)(F2)=(2)(2)1=4
(Assuming the pressure of F2 is 1 atm at standard conditions.)
Substitute the known values into the Nernst equation:
E=5.92−(8.314)(298)(1)(96500)ln(4)
Since ln(4)=2ln(2)=2×0.693=1.386:
E=5.92−(8.314)(298)96500×1.386
First, calculate (8.314)(298)96500:
(8.314)(298)96500≈0.0257 V
Now substitute this back into the equation:
E=5.92−(0.0257×1.386)≈5.92−0.0356≈5.8844 V
Rounding to two decimal places gives:
E≈5.88 V
The voltage of the cell with 2 M LiF electrolyte is approximately 5.88 V.
Topper's Solved these Questions
Similar Questions
Knowledge Check
What is the amount of work done when 0.5 mol of methane, CH4(g) is subjected to combustion at 300K?
(given, R=8.314JK−1mol−1):A−2494 JB−4988 JC+4988 JD+2494 J(ΔH−ΔU) for the formation of carbon monoxide (CO) from its elements at 298 K is :
(R=8.314 JK−1mol−1)A1238.78 J mol−1B−2477.57Jmol−1C2477.57 J mol−1D−1238.78mol−1(ΔH−ΔU) for the formation of carbon monoxide (CO) from its elements at 298 K is (R=8.314kJ−1 mol−1)
A−1238.78Jmol−1B1238.78mol−1C−2477.57Jmol−1D2477.57Jmol−1
Calculate the potential of the following cell reaction at 298 K
Sn4+(1.50M)+Zn(s)→Sn2+(0.50M)+Zn2+(2.0M)
The standard potential, E∘ of the cell is 0.89 V. Whether the potential of the cell will increase or decrease if the concentration of Sn4+ is increased in the cell.
View SolutionSome standard electrode potentials at 298K are given below:
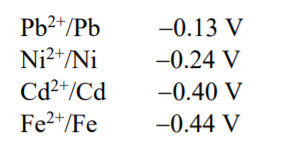
To a solution containing 0.001M of X2+ and 0.1M of Y2+, the metal rods X and Y are inserted (at298K) and connected by a conducting wire. This resulted in dissolution of X. The correct combinations of X and Y, respectively is (are)
(Given: Gas constant, R=8.314JK−1mol−1, Faraday constant,F= 96500Cmol−1)
View SolutionIf the standard electrode potential for a cell is at 300 K, the equilibrium constant (K) for the reaction Zn(s)+Cu2+(aq) at 300 k is approximately : (R=8JK−1mol−1,F=96000mol−1)
View SolutionThe standard emf of a galvanic cell involving cell reaction with n=2 is found to be 0.295V at 25∘C. The equilibrium constant of the reaction would be (GivenF=96,500Cmol−1,R=8.314JK−1mol−1):
View SolutionThe standard emf of a galvanic cell involving cell reaction with n=2 is found to be 0.295 v at 25∘c the equilibrium constant of the reaction would be (Given F= 96500 C mol−1mR=8.314jk−1mol−1 )
View Solution
