If ${Delta}_{1} = | x a x b a a x | a n d {Delta}_{2} = | x b a x |$ are the given determinants, then ${Delta}_{1} = 3 {({Delta}_{2})}_{2}^{2}$ b. $\frac{d}{d x} ({Delta}_{1}) = 3 {Delta}_{2}$ c. $\frac{d}{d x} ({Delta}_{1}) = 3 {({Delta}_{2})}_{2}^{2}$ d. ${Delta}_{1} = 3 Delta 23 / 2$

Video Solution

Answer

Step by step video & image solution for If "Delta"_1=|x bb a x b a a x|a n d"Delta"_2=|x b a x| are the given determinants, then "Delta"_1=3("Delta"_2)^2 b.d/(dx)("Delta"_1)=3"Delta"_2 c. d/(dx)("Delta"_1)=3("Delta"_2)^2 d. "Delta"_1=3"Delta"2 3//2 by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 MATHS DETERMINANTS

Knowledge Check

Question 1 - Select One
If $Δ_{1} = ∣ ∣ ∣ \begin{matrix} 1 & 0 a & b \end{matrix} ∣ ∣ ∣$ and $Δ_{2} = ∣ ∣ ∣ \begin{matrix} 1 & 0 c & d \end{matrix} ∣ ∣ ∣$ , then $Δ_{2} Δ_{1}$ is equal to :
Aac
Bbd
C(b-a)(d-c)
DNone of these
Question 2 - Select One
A substance is carried through the following transformations:

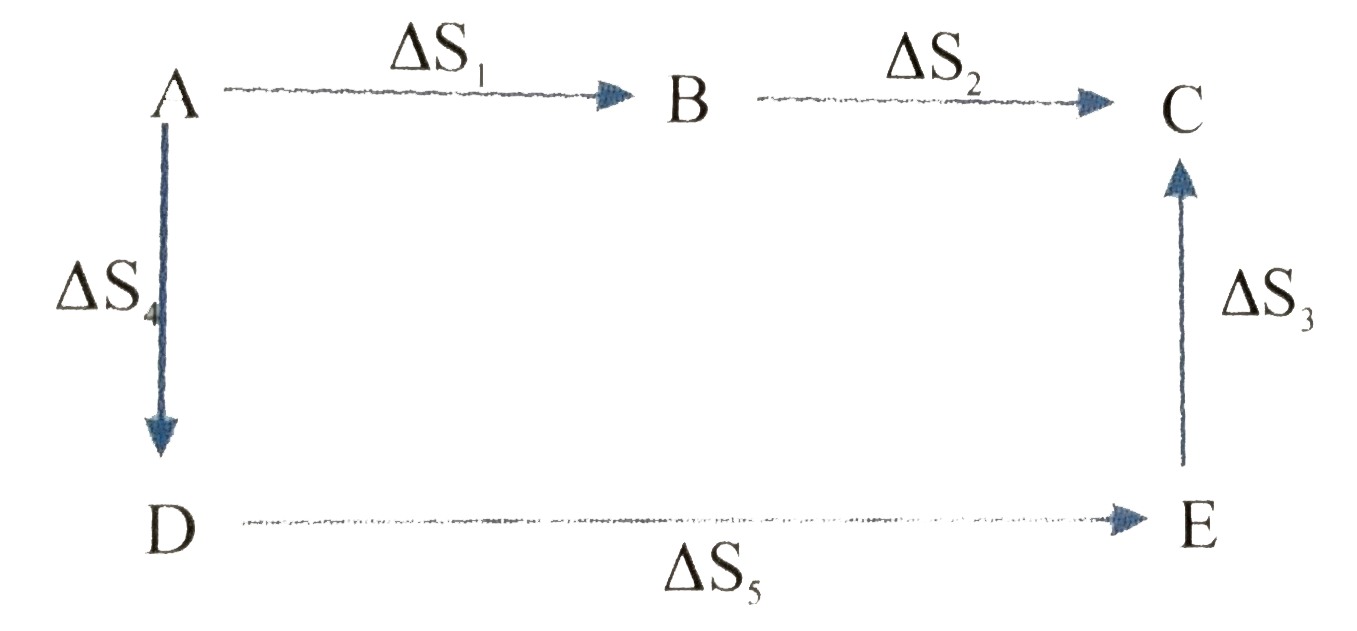
The equation $Δ S_{1} + Δ S_{2} = Δ S_{3} + Δ S_{4} + Δ D_{5}$
AIs true only if the steps are carried out reversibly
BIs always true because entropy is a state function
CMay be true but need more information on the processes
DIs incorrect
Question 3 - Select One
If $Δ = ∣ ∣ ∣ ∣ ∣ \begin{matrix} x & x^{2} & x^{3} 1 & 2 x & 3 x^{2} 0 & 2 & 6 x \end{matrix} ∣ ∣ ∣ ∣ ∣$ then $\frac{d}{d x} (Δ) =$
A6
B6x
C $6 x^{2}$
D0

If ${Delta}_{1} = | x a x b a a x | a n d {Delta}_{2} = | x b a x |$ are the given determinants, then ${Delta}_{1} = 3 {({Delta}_{2})}_{2}^{2}$ b. $\frac{d}{d x} ({Delta}_{1}) = 3 {Delta}_{2}$ c. $\frac{d}{d x} ({Delta}_{1}) = 3 {({Delta}_{2})}_{2}^{2}$ d. ${Delta}_{1} = 3 Delta 23 / 2$

Similar Questions

Knowledge Check

If $Δ_{1} = ∣ ∣ ∣ \begin{matrix} 1 & 0 a & b \end{matrix} ∣ ∣ ∣$ and $Δ_{2} = ∣ ∣ ∣ \begin{matrix} 1 & 0 c & d \end{matrix} ∣ ∣ ∣$ , then $Δ_{2} Δ_{1}$ is equal to :

A substance is carried through the following transformations:

The equation $Δ S_{1} + Δ S_{2} = Δ S_{3} + Δ S_{4} + Δ D_{5}$

If $Δ = ∣ ∣ ∣ ∣ ∣ \begin{matrix} x & x^{2} & x^{3} 1 & 2 x & 3 x^{2} 0 & 2 & 6 x \end{matrix} ∣ ∣ ∣ ∣ ∣$ then $\frac{d}{d x} (Δ) =$

Recommended Questions

If Delta1=|xaxbaax|andDelta2=|xbax| are the given determinants, then Delta1=3(Delta2)2 b.ddx(Delta1)=3Delta2 c. ddx(Delta1)=3(Delta2)2 d. Delta1=3Delta23/2

Similar Questions

Knowledge Check

If Δ1=∣∣∣10ab∣∣∣ and Δ2=∣∣∣10cd∣∣∣, then Δ2Δ1 is equal to :

A substance is carried through the following transformations: The equation ΔS1+ΔS2=ΔS3+ΔS4+ΔD5

If Δ=∣∣ ∣ ∣∣xx2x312x3x2026x∣∣ ∣ ∣∣ then ddx(Δ)=

Recommended Questions

If ${Delta}_{1} = | x a x b a a x | a n d {Delta}_{2} = | x b a x |$ are the given determinants, then ${Delta}_{1} = 3 {({Delta}_{2})}_{2}^{2}$ b. $\frac{d}{d x} ({Delta}_{1}) = 3 {Delta}_{2}$ c. $\frac{d}{d x} ({Delta}_{1}) = 3 {({Delta}_{2})}_{2}^{2}$ d. ${Delta}_{1} = 3 Delta 23 / 2$

If $Δ_{1} = ∣ ∣ ∣ \begin{matrix} 1 & 0 a & b \end{matrix} ∣ ∣ ∣$ and $Δ_{2} = ∣ ∣ ∣ \begin{matrix} 1 & 0 c & d \end{matrix} ∣ ∣ ∣$ , then $Δ_{2} Δ_{1}$ is equal to :

A substance is carried through the following transformations:

The equation $Δ S_{1} + Δ S_{2} = Δ S_{3} + Δ S_{4} + Δ D_{5}$

If $Δ = ∣ ∣ ∣ ∣ ∣ \begin{matrix} x & x^{2} & x^{3} 1 & 2 x & 3 x^{2} 0 & 2 & 6 x \end{matrix} ∣ ∣ ∣ ∣ ∣$ then $\frac{d}{d x} (Δ) =$