A car moves from A to B on a straight road and returns From B to the mid-point of AB=2BC=10cm.Find the displacement and distance covered.
To solve the problem step by step, we will first identify the points and distances involved in the car's journey.
Step 1: Identify the Points and Distances
- Let point A be the starting point.
- Point B is the endpoint of the first leg of the journey.
- Point C is the midpoint of segment AB.
- According to the problem, the distance AB = 10 cm and since 2BC = AB, we can deduce that BC = 5 cm.
Step 2: Calculate the Displacement
Displacement is defined as the shortest distance from the initial position to the final position. In this case:
- The initial position is point A.
- The final position is point C.
The distance AC can be calculated as:
- AC = AB - BC = 10 cm - 5 cm = 5 cm.
Thus, the displacement from A to C is:
- Displacement = 5 cm.
Step 3: Calculate the Total Distance Covered
The total distance covered by the car includes the distance from A to B and then from B to C:
- Distance from A to B = AB = 10 cm.
- Distance from B to C = BC = 5 cm.
Therefore, the total distance covered is:
- Total Distance = AB + BC = 10 cm + 5 cm = 15 cm.
Summary of Results
- Displacement = 5 cm.
- Total Distance Covered = 15 cm.
- Let point A be the starting point.
- Point B is the endpoint of the first leg of the journey.
- Point C is the midpoint of segment AB.
- According to the problem, the distance AB = 10 cm and since 2BC = AB, we can deduce that BC = 5 cm.
Displacement is defined as the shortest distance from the initial position to the final position. In this case:
- The initial position is point A.
- The final position is point C.
- AC = AB - BC = 10 cm - 5 cm = 5 cm.
- Displacement = 5 cm.
The total distance covered by the car includes the distance from A to B and then from B to C:
- Distance from A to B = AB = 10 cm.
- Distance from B to C = BC = 5 cm.
- Total Distance = AB + BC = 10 cm + 5 cm = 15 cm.
- Displacement = 5 cm.
- Total Distance Covered = 15 cm.
Topper's Solved these Questions
- KINEMATICSBOOK - FIITJEECHAPTER - KINEMATICSEXERCISE - Problem (subjective)
10 Videos
- KINEMATICSBOOK - FIITJEECHAPTER - KINEMATICSEXERCISE - Problem (objective)
14 Videos
- HEAT AND TEMPERATUREBOOK - FIITJEECHAPTER - HEAT AND TEMPERATUREEXERCISE - NUMERICAL BASES QUESTIONS
1 Videos
- LAWS OF MOTIONBOOK - FIITJEECHAPTER - LAWS OF MOTIONEXERCISE - COMPREHENSION-III
2 Videos
Similar Questions
Knowledge Check
A person moves through 100m in going from A to B and travels the same distance in returning from B to A. This displacement is
A100mB200mC100√2mDzeroA car travels a distance d on a straight road in two hours and then returns to the starting point in next three hours. Its average speed is:-
Ad5B2d5Cd2+d3DNone of theseA particle moves from A to B in a circular path of radius R covering an angle θ as shown in figure. Find the ratio of magnitude of distance and magnitude of displacement of the particle.
 Aθ2.sinθBθ2sin.θ2Cθ2sinθDθsin.θ2
Aθ2.sinθBθ2sin.θ2Cθ2sinθDθsin.θ2
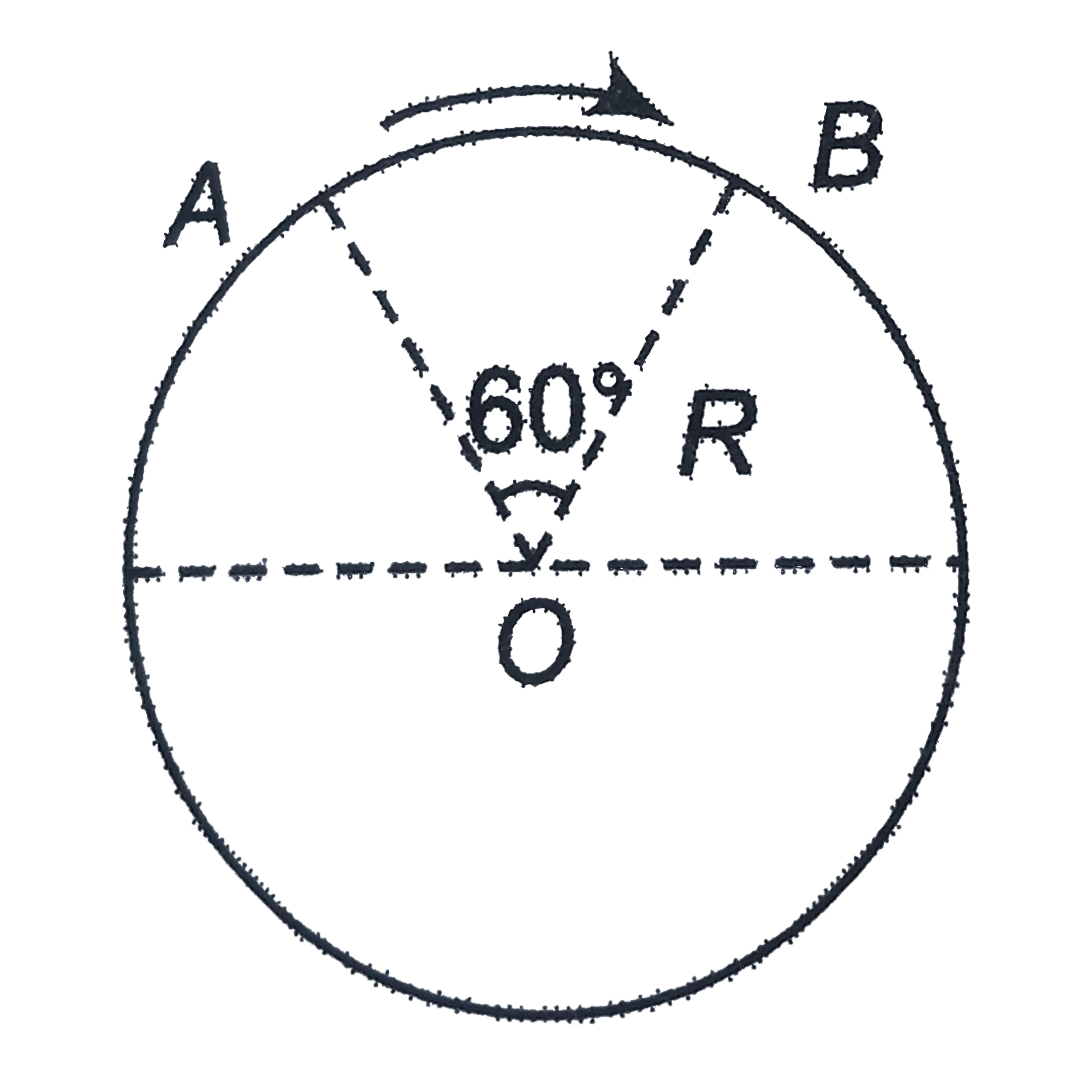
A particle moves in a of radius R from A to B, as shown in the figure. Find the distance and displacement covered.
View SolutionA scooter is moving along a straight line AB covers a distance of 360 m in 24 s and returns back from B to C and coveres 240 m in 18 s. Find the total distance travelled by the scooter.
View SolutionPaheli moves on a straight road from point A to point C. She takes 20 minutes to cover a certain distance AB and 30 minutes to cover the rest of distance BC. She then turns back and takes 30 minutes to cover the distance CB and 20 minutes to cover the rest of the distance to her starting point. She makes 5 rounds on the road the same way. Paheli concludes that her motion is
View SolutionA car is moving on a straight road covers one third of the distance with a speed of 20 km/h and the rest with a speed of 60 km/h. The average speed of the car is
View SolutionA racing car accelerates on a straight road from rest to a speed of 50 mis in 25 s. Assuming uniform acceleration of the car throughout, the distance covered in this time will be
View Solution
