A bead is sliding down a smooth wire tightly stretched between the points P1 and P2 on a vertical circle of radius R. If the bead starts from rest from P1, the highest point on the circle and P2 lies anywhere on the circumference of the circle. Then
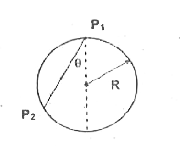
time taken by bead to go from P1 to P2 is dependent on position P2 and equals 2√Rgcosθ
time taken by bead to go from P1 to P2 is independent of position P2 and equals 2√Rg
Acceleration of bead along the wire is g cos θ.
Velocity of bead when it arrives at P2 is 2√gRcosθ.
The correct Answer is:B,C,D
Step by step video, text & image solution for A bead is sliding down a smooth wire tightly stretched between the points P_(1) and P_(2) on a vertical circle of radius R. If the bead starts from rest from P_(1), the highest point on the circle and P_(2) lies anywhere on the circumference of the circle. Then by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- KINEMATICSBOOK - FIITJEECHAPTER - KINEMATICSEXERCISE - ASSIGNMENT PROBLEMS (OBJECTIVE) LEVEL-II (COMPREHENSIONS-I)
3 Videos
- KINEMATICSBOOK - FIITJEECHAPTER - KINEMATICSEXERCISE - ASSIGNMENT PROBLEMS (OBJECTIVE) LEVEL-II (COMPREHENSIONS-II)
3 Videos
- KINEMATICSBOOK - FIITJEECHAPTER - KINEMATICSEXERCISE - ASSIGNMENT PROBLEMS (OBJECTIVE) LEVEL-I (ASSERTION REASONING TYPE)
2 Videos
- HEAT AND TEMPERATUREBOOK - FIITJEECHAPTER - HEAT AND TEMPERATUREEXERCISE - NUMERICAL BASES QUESTIONS
1 Videos
- LAWS OF MOTIONBOOK - FIITJEECHAPTER - LAWS OF MOTIONEXERCISE - COMPREHENSION-III
2 Videos
Similar Questions
A bead is free to slide down on a smooth wire rightly stretched between points AandB on a vertical circle of radius 10m. Find the time (in sec) taken by the bead to reach point B, if the bead slides from rest from the highest point A on the circle.
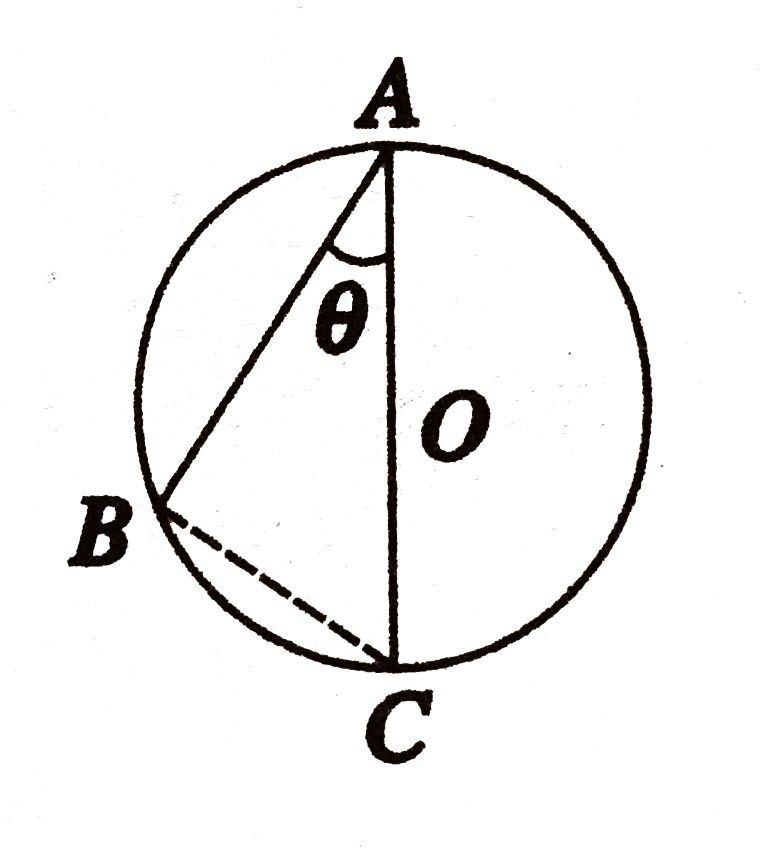 .
.
View SolutionA circular wire frame is fixed in a vertical plane. A smooth wire is tightly stretched between point P1andP2. A bead slides from the point P1 the highest point of the circle Determine (a) its velocity v when it arrives at P2 and (b) show that time to slide along any similar chord is same

View Solution
Knowledge Check
A bead is free to slide down a smooth wire tightly stretched between points A and on a verticle circle of radius R. if the bead starts from rest at 'A', the highest point on the circle, its velocity when it arrives at B is :-
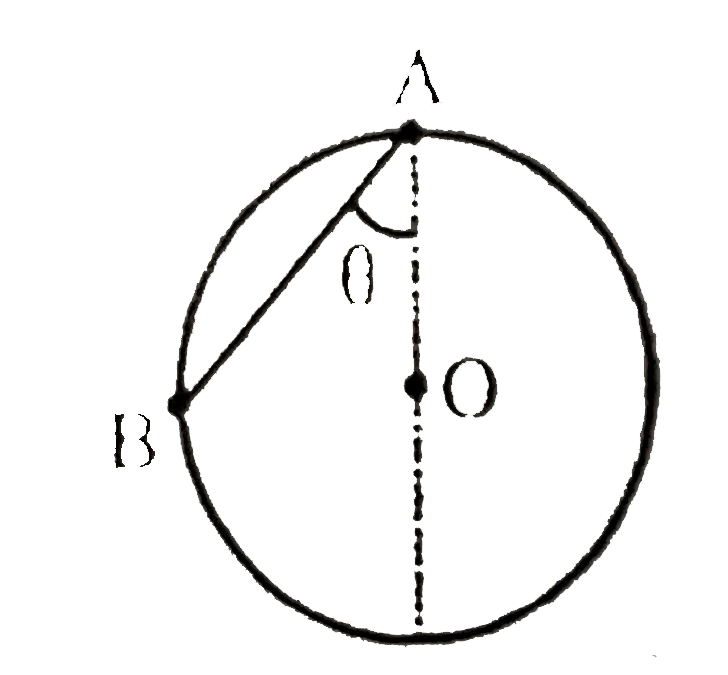 A2√gRB2√gRcosθC2√RgDNone of these
A2√gRB2√gRcosθC2√RgDNone of theseA bead is free to slide down a smooth wire tightly stretched between points A and B on a vertical circle. If the starts from rest at A, the heighest point on the circle
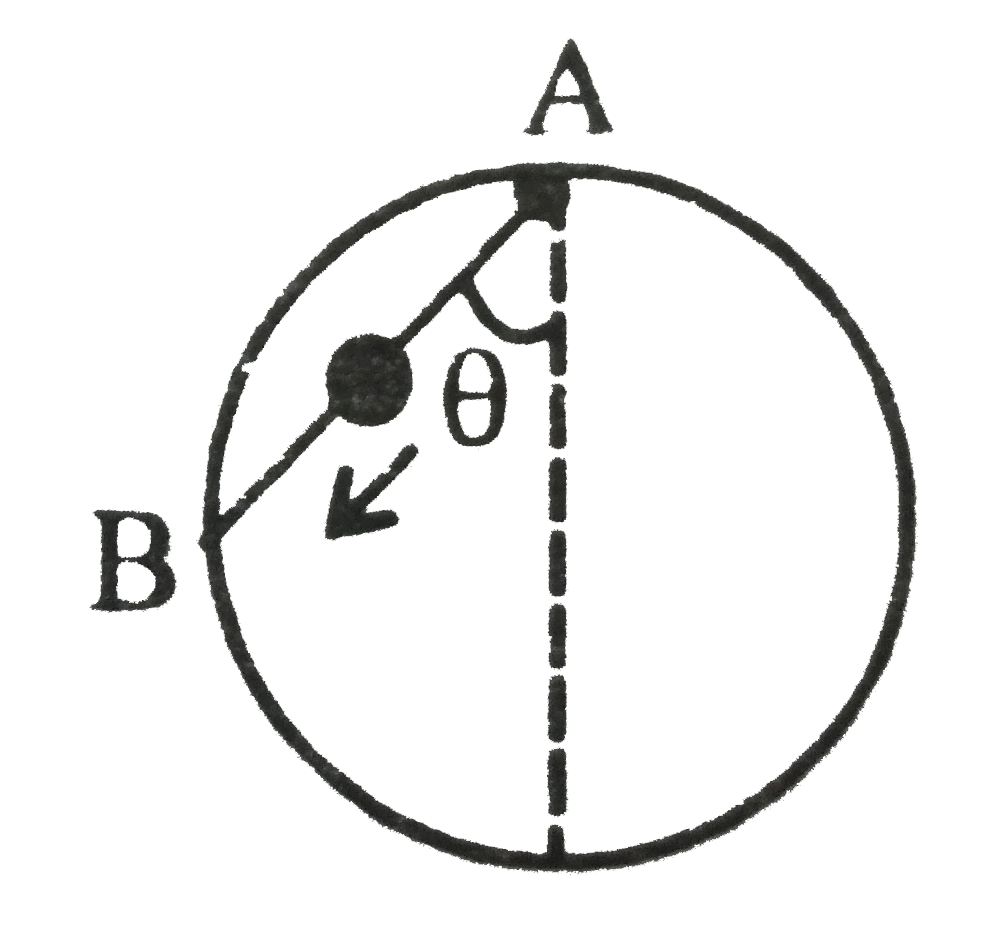 Aits velocity v on arriving at b is proportional to cosθBits velocity v on arriving at B is proportional to tanθCtime to arrive at B is proportional to cosθDtime to arrive at B is independent of θ
Aits velocity v on arriving at b is proportional to cosθBits velocity v on arriving at B is proportional to tanθCtime to arrive at B is proportional to cosθDtime to arrive at B is independent of θO is the centre of a circle. There is a point P in the region of the circle. If PA = PB = PC where A, B and C are points on the circumference of the circle, then OP must be equal to :
APA+PB+PC3BPA+PB+PC2CAB+BC2Dzero
The points P (-2,4) lies on a circle of radius 6 and centre (3,5).
View SolutionDraw a circle of radius 2.5 cm. Take a point at a distance of 5 cm from the centre of the circle. From point P, draw two tangents to the circle.
View SolutionDraw a circle of radius 3 cm. Take a point P on the circle. At point P, construct a tangent to the circle.
View SolutionDraw a circle of radius 3 cm. Take a point P at a distance of 5 cm from the centre of the circle. From P, construct a pair of tangents to the circle.
View SolutionThe time a body takes to slide down any smooth chord of a vertical circle, which is drawn from the highest point of the circle is constant.
View Solution
